Стаж работы рабочих цеха

Стаж работы, лет (х)	до 6	6-12	свыше 12
Число рабочих (f)

Определить средний стаж рабочих цеха.

Он равен:

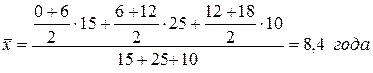
Средняя гармоническая представляет собой обратную величину средней арифметической из обратных величин. Она бывает простая и взвешенная:

простая – ,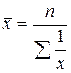

взвешенная – .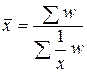

Средняя квадратическая используется в том случае, когда необходимо возводить варианты в квадрат:

простая – ,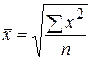

взвешенная – .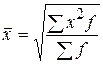

Средняя квадратическая применяется в технике, для расчета среднего квадратического отклонения.

Средняя геометрическая –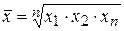

Средняя хронологическая:

простая – ;

(Она применяется в том случае, когда интервалы времени между явлениями равны).

взвешенная – ;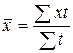

(Она применяется в том случае, когда интервалы времени между явлениями неравны).

Свойства средней арифметической.

1. Средняя арифметическая из постоянных чисел равна этому постоянному числу.

Пусть х = a, тогда

.

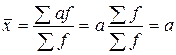2. Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно и то же число раз, то средняя арифметическая нового ряда от этого не изменится. Пусть f уменьшим в к раз. Тогда

.

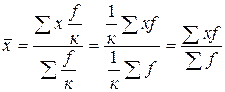3. Если все варианты уменьшить или увеличить на какое-либо число, то средняя арифметическая нового ряда уменьшится или увеличится на столько же.

Уменьшим все варианты х на а, т.е. 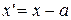. Тогда

.

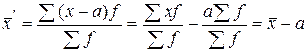Среднюю арифметическую первоначального ряда можно получить, прибавляя к средней арифметической нового ряда, ранее вычтенное из вариантов число a, т.е.

.

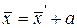4. Если все варианты уменьшить в к раз, то средняя арифметическая нового ряда уменьшится в к раз.

Пусть 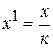, тогда .

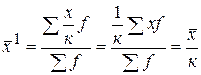Среднюю арифметическую первоначального ряда можно получить, увеличив среднюю арифметическую нового ряда в раз:

.

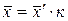5. Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна нулю.

.

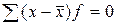Перечисленные свойства позволяют в случае необходимости упрощать расчеты путем замены абсолютных частот относительными, уменьшать варианты на какое-либо число а, сокращать их в к раз и рассчитывать среднюю арифметическую из уменьшенных вариантов, а затем переходить к средней первоначального ряда. Способ исчисления средней арифметической с использованием ее свойств известен в статистике как способ «условного нуля» или «условной средней», а также как «способ моментов».

Этот способ расчета находит отражение в следующей формуле:

.

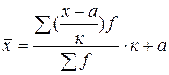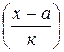
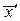Если уменьшенные варианты обозначить через, то

.

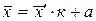Для характеристики среднего значения признака в вариационном ряду используется средняя арифметическая, мода и медиана.

Мода – это наиболее часто встречающееся значение признака в совокупности. Медианой называется численное значение признака, расположенное в середине ранжированного ряда, которое делит этот ряд на две равные по численности части. Для определения медианы сначала находят ее место в ряду по формуле 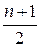, где n – число членов ряда (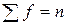). Если число единиц чётное, то место медианы в ряду определяется как .

Применяется мода при экспертных оценках, при установлении размера изделий, который пользуется наибольшим спросом (одежда, обувь), медиана используется при статистическом контроле качества продукции.

Пример.

Таблица 14

Дата добавления: 2014-01-07