Основные аксиомы статики

Условия, при которых тело может находиться в равновесии, выводятся из нескольких основных положений, принимаемых без доказательств, но подтвержденных опытом и называемых аксиомами статики.

Аксиомы статики устанавливают основные свойства сил, приложенных к абсолютно твёрдому телу.

Первая аксиома, называемая законом инерции Галилея-Ньютона, была впервые сформулирована Г. Галилеем в 1638 г.: Система сил, приложенная к материальной точке, является уравновешенной, если под её воздействием точка находится в состоянии относительного покоя или движется равномерно и прямолинейно.

Рассматривая первую аксиому, нетрудно установить, что уравновешенная система сил эквивалентна нулю. Очевидно также, что любая сила уравновешенной системы является уравновешивающей по отношению ко всем остальным силам системы.

Тело (в отличие от точки) под действием уравновешенной системы не всегда находится в покое или движется равномерно и прямолинейно. Возможен случай, когда уравновешенная система сил вызывает равномерное вращение тела вокруг некоторой неподвижной оси.

Следовательно, если на тело действует уравновешенная система сил, то тело либо находится в состоянии относительного покоя, либо движется равномерно и прямолинейно, либо, наконец, равномерно вращается вокруг неподвижной оси.

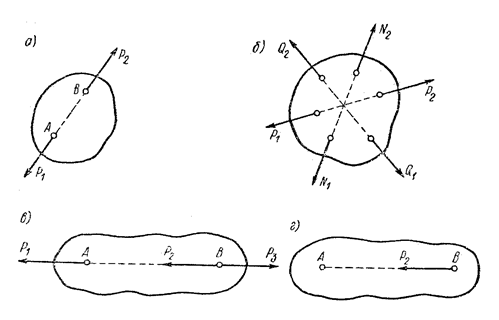
Рис. 2

Вторая аксиома устанавливает условие равновесия двух сил.

Две равные по модулю (величине) силы (Р₁ = Р₂), приложенные к абсолютно твёрдому телу и направленные по одной прямой в противоположные стороны, взаимно уравновешиваются (рис.2, а).

Третья аксиома служит основой для преобразования системы сил.

Не нарушая механического состояния абсолютно твёрдого тела, к нему можно приложить или отбросить от него уравновешенную систему сил.

Тело (рис.2, б) находится в состоянии равновесия. Если к нему приложить несколько взаимно уравновешенных сил - Р₁ = Р₂, Q₁ = Q₂ , N₁ = N₂, - то равновесие тела не нарушится. Аналогичный эффект получится при отбрасывании этих уравновешенных сил.

Системы сил, показанные на рис.2, а, б, эквивалентны, так как они дают одинаковый эффект: под действием каждой из них тело находится в равновесии.

Из второй аксиомы вытекает следствие, согласно которому всякую силу, действующую на абсолютно твёрдое тело, можно перенести вдоль линии её действия в любую точку тела, не нарушив при этом его механического состояния.

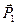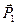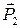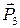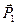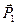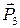Пусть на тело в точке А действует сила (рис.2, в). В произвольной точке В на линии действия силы приложим две силы и , равные по модулю и направленные в противоположные стороны. Состояние тела в этом случае не нарушится, так как силы и , равные по модулю и противоположно направленные, можно отбросить. Таким образом, силу 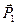можно заменить равной силой 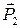, перенесённой по линии действия 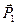из точки А в точку В (рис.2, г).

Векторы, которые можно переносить по линии их действия, называют скользящими. Как показано выше, сила является скользящим вектором.

Четвёртая аксиома служит основой для сложения сил. Равнодействующая двух сил, приложенных к одной точке, приложена в этой точке и равна диагонали параллелограмма, построенного на данных силах. Так, равнодействующей двух сил и 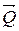, приложенных в точке А (рис.3, а), будет сила 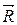, представляющая собой диагональ параллелограмма ACDB, построенного на векторах заданных сил. Определение равнодействующей двух сил по правилу параллелограмма называется векторным, или геометрическим сложением и выражается векторным равенством

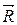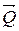= +. (1)

При графическом определении равнодействующей двух сил вместо правила параллелограмма можно пользоваться правилом треугольника. Из произвольной точки А (рис.3, б) проводим, сохраняя масштаб и заданное направление, вектор первой составляющей силы 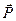, из его конца проводим вектор, параллельный и равный второй составляющей силе 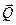. Замыкающая сторона AD треугольника и будет искомой равнодействующей . Её можно также представить как диагональ параллелограмма ABDC, построенного на заданных силах.

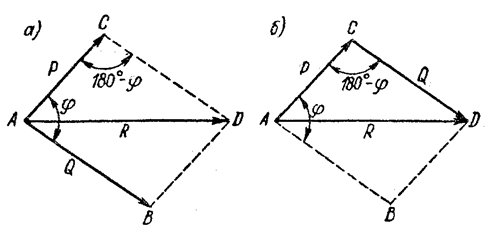
Рис. 3

Модуль равнодействующей двух сил можно определить из ∆ ACD:

R² = P² + Q² – 2PQ cos(180° − φ); cos(180° − φ) = − cos φ,

поэтому R² = P² + Q² + 2PQ cos φ, или R =. (2)

На основании четвёртой аксиомы одну силу 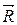можно заменять двумя составляющими силами и 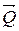. Такую замену часто производят при решении задач статики, заменяя неизвестную (искомую) реакцию 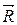её составляющими – проекциями реакции на оси х и у.

Пятая аксиома устанавливает, что в природе не может быть одностороннего действия силы.

Рис. 4

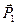При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие. Так, если на тело В (рис. 4) действует сила со стороны материального тела А, то на тело А действует со стороны тела В такая же по величине сила 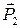. Обе силы действуют по одной прямой и направлены в противоположные стороны. Действие и противодействие всегда приложены к различным телам, и именно поэтому они не могут уравновешиваться.

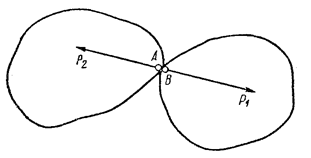
Рис. 4

Дата добавления: 2014-01-07