Основные этапы проведения выборочного наблюдения

Сущность и значение выборочного наблюдения

Выборочные аналоги параметров генеральной совокупности

Выборочное наблюдение - один из наиболее широко приме­няемых видов несплошного наблюдения. При его проведении об­следуются не все единицы изучаемого объекта (генеральной сово­купности), а лишь некоторая, отобранная определенным способом часть этих единиц (выборочная совокупность). Выборка должна быть репрезентативной, то есть правильно отражать пропорции генеральной совокупности. Это достигается случайностью отбора, когда все объекты генеральной совокупности имеют одинаковую вероятность быть отобранными. При этом наблюдение организо­вано таким образом, что эта часть отобранных единиц в уменьшенном масштабе представляет всю совокупность.

Важная роль в формировании выборочного метода принадлежит работам швейцарского математика Якоба Бернулли (1654 - ­1705). Весомый вклад в разработку теоретических основ выбо­рочного метода внесли русские математики – П.Л.Чебышев, А.М. Ляпунов, А.А. Марков. Российская статистика имеет нема­лые заслуги в практическом применении выборочного метода. Так, уже во второй половине XIX в. выборочные обследования проводились земскими статистиками и отличались определенной новизной в решении вопросов организации отбора единиц.

Выделим основные причины, по которым во многих случа­ях выборочному наблюдению отдается предпочтение перед сплошным:

1. при минимальной численности обследуемых единиц про­ведение исследования осуществляется в более короткие сроки и с минимальными затратами труда, материальных и финансовых средств. Это повышает оперативность статистической информа­ции, позволяя провести исследование более тщательно и квали­фицированно и достигнуть большой точности результатов обсле­дования благодаря сокращению ошибок регистрации.

2. Сведение к минимуму порчи или уничтожения исследуемых объектов (особенно при проверке качества продукции).

3. Необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц.

Цель выборочного наблюдения - определение параметров генеральной совокупности на основе параметров выборочной со­вокупности. Разница между генеральными и выборочными пара­метрами называется ошибкой выборки или ошибкой репрезента­тивности. Формулы ее определения, разработанные теорией ве­роятностей и математической статистикой, дифференцированы в зависимости от видов и способов отбора.

Выделяют следующие этапы проведения выборочного на­блюдения:

1) определение необходимого объема выборки и способа отбора;

2) проведение отбора;

3) обобщение данных наблюдения и расчет выборочных ха­рактеристик;

4) расчет ошибок выборки;

5) распространение выборочных характеристик на генеральную совокупность.

Основные характеристики параметров генеральной и выбо­рочной совокупностей обозначаются следующими символами:

N - генеральная совокупность (подлежащая измерению ста­тистическая совокупность, из которой производится отбор части единиц);

п - выборочная совокупность (выборка) (отобранная из ге­неральной совокупности часть единиц, которая подлежит непо­средственному изучению);

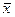- генеральная средняя (среднее значение признака в ге­неральной совокупности);

- выборочная средняя;

- генеральная дисперсия;

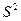- выборочная дисперсия;

р - генеральная доля;

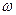- выборочная доля, определяется отношением единиц, обладающих изучаемым признаком (т), к общей численности единиц выборочной совокупности (п):

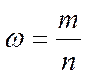(1)

Выборочный метод широко распространен в государствен­ной и ведомственной статистике (например, бюджетные обследо­вания семей рабочих, крестьян и служащих, обследования жи­лищных условий, заработной платы и др.). В торговле с помощью выборочного метода изучаются качество поступивших товаров, эффективность новых форм торговли, спрос населения на опре­деленные виды товаров, степень его удовлетворения и др. Широ­ко используется выборочное наблюдение для исследования сег­ментации рынка, изучение потребностей в рекламной информа­ции и в других областях предпринимательской деятельности.

Вывод по 1-му вопросу: В проведении ряда исследований выборочный метод являет­ся единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожени­ем или разложением на составные части обследуемых образцов (дегустация, определение сахаристости фруктов, клейковины пе­ченого хлеба, проверка электрических лампочек, установление носкости обуви, прочности тканей на разрыв и т. д.), при изуче­нии экономических процессов - уровня жизни населения, рыноч­ных цен, грузо- и пассажиропотоков и т.д.

Все это обусловливает более широкое применение выбороч­ного метода в экономике, прежде всего в торговле, порождающей и потребляющей огромные массивы информации.

Дата добавления: 2014-01-07