Виды и способы отбора в выборочное наблюдение

Основные способы формирования выборочной совокупности

Точность выборки зависит и от схемы отбора. Различают два вида отбора - повторный и бесповторный. Первый соответствует схеме «возвращенного шара»: после отбора какой-либо единицы она возвращается в генеральную совокупность и снова может быть выбранной. Таким образом, вероятность попадания каждой от­дельной единицы в выборку равна 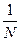, и она остается постоянной на всем протяжении отбора. Такая возможность прежде всего мо­жет иметь место в выборочных обследованиях населения в качест­ве покупателей, пациентов, избирателей, абитуриентов и т.д.

При бесповторной выборке отобранная единица не возвра­щается в генеральную совокупность, поэтому вероятность попа­дания в выборку для оставшихся единиц увеличивается с каждым шагом отбора.

Деление выборки на повторную и бесповторную введено математической статистикой. В социально-экономических исследо­ваниях повторный отбор применяется очень редко.

По степени охвата единиц исследуемой совокупности различают большие и малые (меньше 30) выборки.

В практике наибольшее распространение получили следую­щие способы отбора:

собственно-случайная;

механическая;

типическая (расслоенная или районированная);

серийная (гнездовая);

комбинированная;

многоступенчатая;

многофазная.

1. Собственно-случайная или простая выборка.

Собственно-случайную выборку также называют методом жеребьевки или методом лото. При данном способе отбора ка­ждой единице совокупности присваивается порядковый номер, заносимый на определенные предметы (жетоны, бумажки, фиш­ки, кубики, бочонки, шары или билеты), которые затем переме­шиваются и выбираются наугад. При этих условиях каждая из них имеет одинаковую вероятность попасть в выборку.

Можно использовать и математические таблицы случайных чисел. Для этого берется любая строка или колонка таблицы, и в выборку включаются указанные номера единиц генеральной со­вокупности.

На практике чаще применяются схемы бесповторного слу­чайного отбора. Но в торговле выборочное наблюдение может проводиться по схеме повторного отбора. Например, при изуче­нии покупательского спроса населения не исключена повторная регистрация неудовлетворенного спроса одного и того же лица в нескольких магазинах города.

2. Механическая выборка.

Механическая выборка применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена или ранжирована, то есть имеется определенная последовательность в расположении единиц (списки студентов по алфавиту, телефон­ные номера абонентов, номера домов, квартир, торговых точек и т.д.). Отбор единиц в выборочную совокупность из генеральной, разбитой на равные интервалы или группы, производится таким образом, что из каждой группы в выборку отбирается лишь одна единица. Чем меньше выборка, тем больше интервал. Причем в выборочную совокупность должна отбираться та единица, кото­рая находится в середине каждой группы. Это позволяет избе­жать появления систематической ошибки выборки.

Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осущест­вить, не прибегая к составлению списков, а используя фактиче­ское размещение единиц генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или по­точной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т. д.

Доказано, что механическая выборка по точности результа­тов близко подходит к собственно-случайному способу отбора и бывает только бесповторной.

3. Типическая (районированная) выборка.

При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. При обследова­нии населения такими группами могут быть, например, возрас­тные, социальные, образовательные группы. Затем из каждой ти­пической группы собственно-случайной или механической вы­боркой производится индивидуальный отбор единиц в выборочную совокупность. Типическая выборка обычно применяется при изучении сложных статистических совокупностей.

Например, необходимо провести типический отбор 1500 студентов из 10 000, обучающихся на четырех факультетах института. Для этого их группируют в однородные группы по факультетам, а затем по каждой из них отбирают число студентов пропорцио­нально удельному весу числа студентов института по факультетам. Важной особенностью типической выборки по сравнению с другими способами отбора являются наиболее точные результа­ты. Репрезентативность типической выборки обеспечивается раз­делением генеральной совокупности на качественно однородные группы. Таким образом, чем однороднее состав образованных типических групп, тем лучше типическая выборка будет отра­жать характеристики изучаемого признака в генеральной сово­купности. Различают типическую выборку, пропорциональную объему типических групп, и типическую выборку, пропорцио­нальную внутригрупповой вариации (дифференциации) признака.

4. Серийная или гнездовая выборка.

Серийная выборка - особый способ отбора из генеральной совокупности, когда случайно или механически выбирают не от­дельные единицы, а целые их серии или гнезда, внутри которых ведут сплошное наблюдение. Серии (гнезда) состоят из единиц, связанных между собой или территориально, или организацион­но, или, наконец, во времени. Серии могут быть равновеликими и неравновеликими. В качестве серий можно выделить упаковки и партии товара, студенческие группы, школьные классы, рабочие бригады и т.д.

Применение серийной выборки в торговле связано с тем, что многие товары для их транспортировки, хранения и продажи упаковываются в пачки, коробки, ящики и т. п. Поэтому при кон­троле качества поступившего в упаковке товара рациональнее проверить несколько отдельных упаковок (серий), чем из всех упаковок отобрать необходимое количество единиц товара.

Отбор отдельных серий в выборочную совокупность осуще­ствляется либо посредством собственно случайной выборки, либо механическим отбором. Практически серийная выборка произво­дится по схеме бесповторного отбора.

В качестве примера можно привести и таможенную службу, где выборочно вскрывают каждый сотый контейнер из прибы­вающих в порт, а в нем проверяется полностью весь груз.

По сравнению с типической выборкой серийная выборка дает более высокую ошибку представительности (репрезентативно­сти). Это обусловлено тем, что при серийной выборке, как прави­ло, образуется сравнительно небольшое число серий. Для умень­шения возможной ошибки серийной выборки на практике прихо­дится увеличивать объем обследуемых серий, то есть брать более высокую долю выборки.

5. Комбинированная выборка.

Комбинированная выборка предполагает использование не­скольких способов выборки. Можно комбинировать, например, серийную выборку и случайную. В этом случае, разбив генеральную совокупность на серии (группы) и отобрав нужное число се­рий, производят случайную выборку единиц в серии. Ошибка такой выборки определяется ступенчатостью отбора.

6. Многоступенчатая выборка.

Многоступенчатая выборка предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, за­тем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы (серии) или отдельные единицы, которые будут подвергнуты наблюдению. Выборка может быть двухсту­пенчатой, когда генеральная совокупность разбивается на группы и производится отбор групп, а затем внутри групп - отбор единиц наблюдения. На обеих ступенях отбор может вестись в случай­ном порядке.

При многоступенчатом отборе производится отбор самих групп, и, следовательно, не все они попадают в выборку.

Число ступеней может быть и более трех. Если число ступе­ней отбора больше двух, то средняя ошибка выборки определяет­ся по формуле

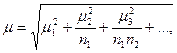(2)

где

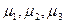- средние ошибки выборки на отдельных ступенях отбора;

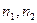- численность выборок на соответствующих сту­пенях.

7. Многофазная выборка.

При многофазной выборке выборочные совокупности обра­зуются таким образом, что одни сведения собираются от всех единиц отбора, затем отбираются еще некоторые единицы, кото­рые и обследуются по более широкой программе. Расчет ошибки многофазной выборки производится для каждой фазы в отдель­ности.

Для статистического изучения протекающих во времени процессов применяются моментные выборочные обследования. Большое распространение этот метод получил при анализе использования рабочего времени. Моментные выборочные обсле­дования менее трудоемки, чем хронометраж или фотография ра­бочего дня, результаты при правильной организации моментных обследований достаточно точные.

Основное содержание метода моментных выборочных об­следований периодическая фиксация (в заранее установленные моменты времени) состояния изучаемой совокупности. При сплошном охвате всех единиц совокупности этот метод по вре­мени получения информации относится к выборочному наблю­дению. При этом генеральной совокупностью является общий фонд рабочего времени, а выборочную совокупность представля­ет сумма фондов рабочего времени, в которых проводилась фик­сация состояния изучаемых признаков. Важнейший вопрос про­ведения моментного выборочного исследования – установление объема выборки.

Дата добавления: 2014-01-07