Средние и предельные ошибки выборочного наблюдения

Одна из задач, решаемая на основе выборочного метода, ­определение ошибки выборки. В статистике принято определять среднюю (стандартную), предельную и относительную ошибки выборочного наблюдения. Ошибки выборки подразделяют на:

- ошибки регистрации, возникающие из-за неправильных или неточных сведений. Источниками таких ошибок могут быть непонимание существа вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности, описки при заполнении анкет, формуляров и т.д. Они достаточно легко обнаруживаются и устраняются. Среди ошибок регистра­ции выделяют:

систематические (тенденциозные) ошибки, зависящие от организации выборочного исследования и обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам, сотням и т.д.);

случайные (непреднамеренные) ошибки, связанные с природой любых статистических погрешностей и проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.

- ошибки репрезентативности, возникающие из-за постоян­ного или спонтанного несоблюдения принципа случайного отбо­ра и которые также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором на­рушается основной принцип научно организованной выборки - принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между характеристиками выбороч­ной и генеральной совокупностей. Избежать ошибок репрезента­тивности нельзя, однако, пользуясь методами теории вероятно­стей, основанными на использовании предельных теорем закона больших чисел, эти ошибки можно свести к минимальным значе­ниям, границы которых устанавливаются с достаточно большой точностью. Изучение и измерение случайных ошибок репрезен­тативности - основная задача выборочного метода.

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки, которые свойственны только выборочным наблюдениям. Данные показа­тели отражают разность между выборочными и соответствую­щими генеральными показателями.

Средняя ошибка выборки определяется прежде всего объе­мом выборки и зависит от структуры и степени варьирования изучаемого признака.

Смысл средней ошибки выборки заключается в следующем. Рассчитанные значения выборочной доли (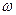) и выборочной средней (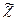) по своей природе случайные величины. Они могут принимать различные значения в зависимости от того, какие кон­кретные единицы генеральной совокупности попадут в выборку.

Например, если при определении среднего возраста работников предприятия в одну выборку включить больше молодежи, а в другую - работников старшего возраста, то выборочные средние и ошибки выборки будут разными. Средняя ошибка выборки оп­ределяется по формуле

(3)- повторная выборка.

Для показателя средней величины дисперсия количественно­го признака в выборке определяется по формулам

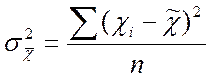; (4)

(5)

При альтернативном или атрибутивном признаке выборочная дисперсия доли определяется по формуле

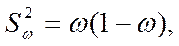(6)

где 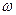- доля единиц, обладающих каким-либо значением при­знака в выборочной совокупности.

Поскольку при бесповторном отборе численность генераль­ной совокупности N в ходе выборки сокращается, то в формулу для расчета средней ошибки выборки включают дополнительный множитель .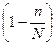

Формула средней ошибки выборки принимает следующий вид:

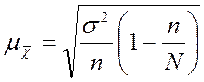. (7)

Средняя ошибка меньше у бесповторной выборки, что и обу­словливает ее более широкое применение.

Для практических выводов нужна характеристика генераль­ной совокупности на основе выборочных результатов. Выбороч­ные средние и доли распространяются на генеральную совокуп­ность с учетом предела их возможной ошибки, причем с гаранти­рующим ее уровнем вероятности. Задавшись конкретным уровнем вероятности, выбирают величину нормированного от­клонения и определяют предельную ошибку выборки. Наиболее полно закономерности случайных ошибок выборки раскрыты в теоремах П.Л. Чебышева и А.М. Ляпунова.

Предельная ошибка выборки (∆) по теореме П.Л.Чебышева представляет собой максимум ошибок при заданной вероятности ее появления или t-кратную среднюю ошибку:

∆=tμ (8)

Если в формулу подставить конкретное содержание средней ошибки μ, то расчет предельной ошибки выборки при бесповтор­ном отборе можно записать следующими алгоритмами:

а) доля альтернативного признака:

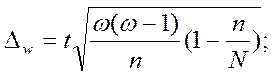(9)

б) средняя величина количественного признака:

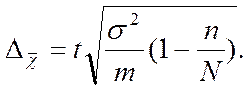(10)

А.М. Ляпунов дал выражение конкретных значений множи­теля t для различных степеней вероятности в виде функции:

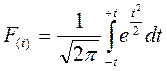(11)

На практике пользуются готовыми таблицами этой функции, вычисленными для различных значений t применительно к слу­чаю нормально распределенной совокупности.

В экономических и товароведческих исследованиях обычно ограничиваются значениями t, не превышающими двух-трех единиц. При этом выбор той или иной доверительной вероятности зависит от того, с какой степенью достоверности требуется га­рантировать результаты выборочного обследования.

t-Коэффициент доверия определяется, по таблице значений интегральной функции Лапласа при заданной доверительной ве­роятности. Приведем наиболее часто употребляемые уровни до­верительной вероятности и соответствующие им значения t:

P(t)	0,683	0,950	0,954	0,990	0,997
t	1,00	1,96	2,00	2,58	3,00

Появление ошибки большей, чем утроенная средняя ошибка выборки, имеет крайне малую вероятность (1 - 0,997 = 0,003) и считается практически невозможным событием.

Зная величину выборочной средней (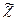) или доли (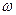), а так­же предельную ошибку выборки (∆), можно определить доверительные интервалы, в которых находятся значения генеральных параметров:

Доказано, что при случайном и механическом отборах сред­няя ошибка выборки для средней величины () определяется следующим образом:

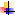при повторном отборе: (12)

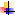при бесповторном отборе: 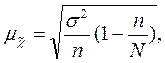(13)

где 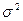- дисперсия признака в генеральной совокупности;

п - численность выборки; N - численность генеральной совокупности.

Формулы для расчета средней ошибки выборочной доли соот­ветственно для повторного и бесповторного отборов имеют вид:

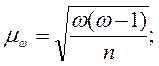(14)

(15)

Для типической выборки средняя ошибка вычисляется по формулам:

- при отборе, пропорциональному объему типических групп:

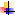повторный отбор:

(16)

где 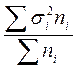- средняя из внутригрупповых дисперсий;

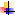бесповторный отбор:

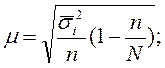(17)

- при отборе, пропорциональном вариации признака:

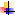повторный отбор

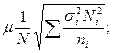( 18)

бесповторный отбор

(19)

где и 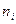- объёмы i-й типической группы и выборки из нее соответственно; 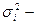групповые дисперсии.

При серийной выборке средняя ошибка определяется следующим образом:

повторный отбор:

(20)

бесповторный отбор:

(21)

где R – число серий в генеральной совокупности;

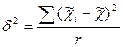- межгрупповая (межсерийная) дисперсия;

r – число серий в выборочной совокупности.

Дата добавления: 2014-01-07