Средневзвешенные индексы

Помимо записи общих индексов в агрегатном виде в практи­ке статистики часто используют формулы их расчета как вели­чин, средних из соответствующих индивидуальных индексов.

Средневзвешенный индекс - средняя величина из индивиду­альных индексов. При его расчете используются две формы средних величин: арифметическая и гармоническая. Применение той или иной формулы средневзвешенного индекса зависит от имеющейся в распоряжении информации.

Средний гармонический индекс цен применяется в тех случа­ях, когда неизвестны отдельные значения 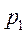и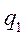, но дано их про­изведение 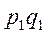и индивидуальные индексы цен 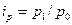, а свод­ный индекс должен быть исчислен с отчетными весами. Индиви­дуальные индексы должны быть взвешены таким образом, чтобы средний гармонический индекс совпал с агрегатным.

Выражая из формулы индивидуальных индексов цен неиз­вестное значение 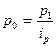, подставляем его в знаменатель агре­гатной формулы и получаем средний гармонический индекс цен, который равен формуле Пааше:

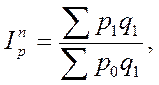
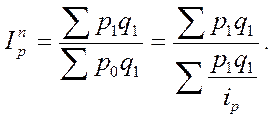
Так как 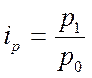, то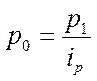

Весами индивидуальных индексов 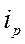в данном индексе явля­ется стоимость отдельных видов продукции отчетного периода в ценах того же периода .

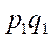Средний арифметический индекс цен получается в том слу­чае, если из индивидуального индекса цен 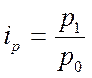выразить це­ну отчетного периода 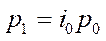, а затем подставить ее в числитель агрегатного индекса цен. Данный индекс тождествен агрегатному индексу Ласпейреса и имеет следующий вид:

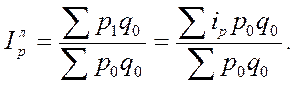
Для построения средневзвешенного физического объема про­дукции в качестве базы необходимо брать его агрегатную форму:

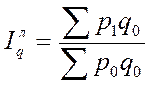
Из формулы индивидуального индекса физического объема продукции 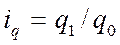находим 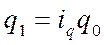. Подставляя полученное уравнение в формулу, получим общий индекс физического объе­ма в форме среднего арифметического индекса физического объ­ема продукции, где весами является стоимость отдельных видов продукции в базисном периоде ( ):

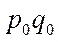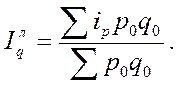
Если фактическую стоимость каждого вида продукции раз­делить на соответствующий индивидуальный индекс физическо­го объема и подставить полученное выражение в знаменатель исходной формулы, то получим средний гармонический взвешен­ный индекс физического объема продукции:

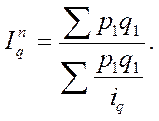
Средние индексы широко применяются для анализа состоя­ния рынка ценных бумаг. Индикаторы рынка ценных бумаг рас­считываются по их видам: акции, облигации, опционы и др. Можно выделить следующие интегральные показатели: индексы Доу-Джонса, индекс Стендарта и Пура.

2.5. Индексный анализ средних величин: индексы постоянного, переменного составов и структурных сдвигов

Все рассмотренные выше индексы рассчитывались по не­скольким товарам, реализуемым в пределах одной территории, или нескольким видам продукции, про изводимым на одном предприятии. Рассмотрим случай, когда один товар реализуется в нескольких местах или один вид продукции производится на ряде предприятий. Для однородной совокупности возможно использо­вание средних значений, общее изменение которых обусловлено взаимодействием двух факторов: изменением отдельных уровней показателя и изменением в структуре весов.

Под изменением структуры здесь понимают изменение доли отдельных единиц совокупности, из которых формируются сред­ние в общей их численности. Например, динамика среднедуше­вого дохода населения зависит от изменения среднего дохода ка­ждого человека и от изменения количества людей с более высо­кими и низкими доходами в общей численности; средняя цена на хлеб может изменяться не только под влиянием изменения цены хлеба, но и в результате изменения состава товарной массы. Эта задача решается с помощью индексного метода, то есть путем построения системы взаимосвязанных индексов. Система вклю­чает три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индекс переменного состава представляет собой соотноше­ние средних величин какого-либо признака в отчетном и базис­ном периодах:

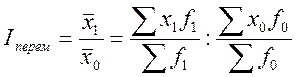
Данный индекс характеризует не только изменение индиви­дуальных цен в местах продажи, но и изменение структуры реа­лизации по предприятиям розничной и оптовой торговли, рын­кам, городам и регионам.

Индекс, характеризующий динамику средней величины при одной и той же фиксированной структуре какой-либо однородной совокупности, то есть когда влияние структурного фактора уст­ранено, называется индексом постоянного (фиксированного) со­става и может быть вычислен по формуле

Индекс постоянного состава может быть рассчитан и в агре­гатной форме:

Индекс структурных сдвигов необходим для измерения влияния только структурных изменений на исследуемый средний показатель и может быть рассчитан по формуле

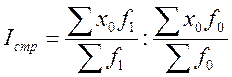
Индексы переменного, постоянного состава и структурных сдвигов увязываются в следующую систему:

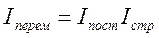
Если в индексах средних уровней в качестве весов использу­ются удельные веса единиц совокупности в общей численности совокупности, то есть показатели доли (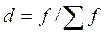), то система ин­дексов может быть записана в следующем виде:

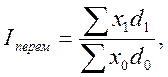
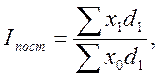
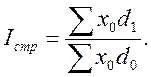
Система индексов переменного, постоянного состава и струк­турных сдвигов строится для изучения динамики среднего уровня цен, себестоимости, фондоотдачи, рентабельности, производитель­ности труда, заработной платы и других вторичных признаков.

Выводы по 2-му вопросу: В статистической практике индексный метод имеет такое же широкое распространение, как и метод средних величин. Индекс - это результат сравнения двух одноименных показателей, при исчислении которого следует различать числитель индексного отношения (сравниваемый или отчетный уровень) и знаменатель индексного отношения (базисный уровень, с которым производится сравнение). Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана. Индексы формируют важнейшие экономические показатели национальной экономики и ее отдельных отраслей. Индексные показатели позволяют осуществить анализ результатов деятельности предприятий и организаций, выпускающих самую разнообразную продукцию или занимающихся различными видами деятельности. С помощью индексов можно проследить роль отдельных факторов при формировании важнейших экономических показателей, выявить основные резервы производства. Индексы широко используются в сопоставлении международных экономических показателей при определении уровня жизни, деловой активности, ценовой политики и т.д. Существует два подхода в интерпретации возможностей индексных показателей: обобщающий (синтетический) и аналитический, которые в свою очередь определяются разными задачами.

Выводы по лекции:

Исследование объективно существующих связей между явлениями – важнейшая задача общей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявить факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативными и множеством факторных признаков (при многофакторной связи).

Индексы относятся к важнейшим обобщающим показателям. С помощью экономических индексов решаются следующие задачи: измерение социально-экономического явления за два и более периода времени; измерение динамики среднего экономического показателя; изменение показателей по разным регионам и т.д.

Дата добавления: 2014-01-07