Особенности конструкций уплотнительных узлов поршня и штока гидроцилиндра для приводов, работающих длительное время при высоком давлении жидкости)

Литература:

2.1 Ю.Г. Оболенский, С.А. Ермаков, Р.В. Сухоруков. Введение в проектирование авиационных рулевых приводов. // Официальное учебное пособие по специальности 160603 «Системы приводов летательных аппаратов» М. Изд. ГУП ЮЗАО. 2011 г.

Тема 3. Динамические свойства системы рулевого привода с учётом жесткости установочных узлов привода.

Гидравлические следящие приводы широко применяются в авиационной и ракетной технике для управления рулевыми поверхностями самолетов, разворотом шасси, воздухозаборниками двигателей, поворотом сопел реактивных двигателей и газовыми рулями ракет, радиолокационными антеннами и другими инерционными объектами. Органы управления летательных аппаратов (рулевые поверхности, сопла реактивных двигателей и т.п.) представляют собой инерционные объекты значительной массы с упругими механическими связями. Рулевые приводы, управляющие положением инерционных объектов, часто обладают малым собственным демпфированием и большой массой. При установке на летательный аппарат рулевые приводы устанавливаются на упругое основание, а выходное звено приводов связано с центром масс инерционного объекта (рулевой поверхности или сопла ракетного двигателя) посредством некоторой упругой конструкции. Указанные выше упругости не являются преднамеренными, а являются следствием стремления конструкторов ограничить вес летательного аппарата. Диссипативными факторами в таких механических системах (факторами рассеяния кинетической энергии) являются трение в подшипниках и конструкционное трение при деформации конструкции.

Рассмотрим динамику упругой рулевой поверхности при ступенчатом силовом воздействии. Например, пусть поверхность закручивается под действием силы Fн, как это показано на рис.3.1.

Определим обобщённые параметры рулевой поверхности, как объекта управления. Упругость механической связи поршня с центром масс инерционного объекта можно пересчитать в жесткость проводки Спр; момент инерции J – в приведенную к поршню массу М, шарнирный момент в произведение коэффициента шарнирного момента 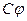на отклонение рулевой поверхности 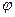, а суммарные силы трения силы – в коэффициент силы вязкого трения hy.

После снятия действия внешней силы поверхность совершает свободные движения в переходном процессе, который показан на рис.3.2. На рис.3.3 приведены линейные уравнения, которые приближённо описывают движение центра масс инерционного объекта.

Рис.3.1

Схема для выходной части рулевого привода с упругой рулевой поверхностью для оценки её динамических свойств.

Эти уравнения не учитывают конструкционное трение в инерционном объекте. Поэтому затухание переходного процесса на каждом периоде движения центра масс неодинаково. На этом же рисунке (вправо) показан приближённый график зависимости меры демпфирования (логарифмического декремента затухания) от номера периода переходного процесса. Упругость элементов конструкции летательного аппарата, на которых крепится рулевой привод, и упругость собственно рулевой поверхности приводят к тому, что при формировании расчетной схемы конструкция привода представляется в виде упруго-массовой системы с эквивалентной жесткостью опоры C_0п, на которую крепится привод, и эквивалентной жесткостью механической передачи от поршня к центру масс органа управления C_пр.

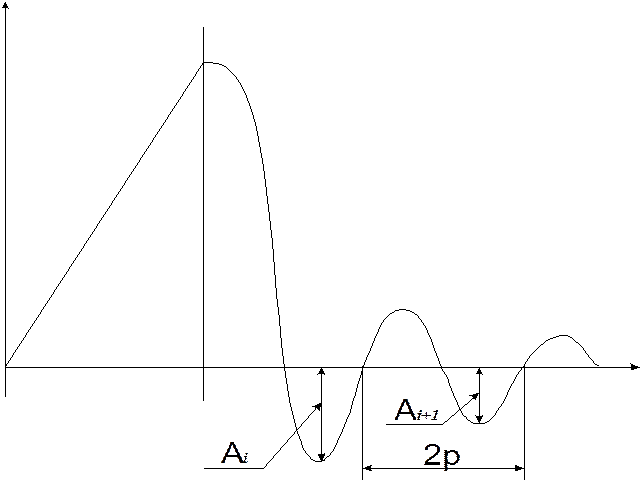
Рис.3.2

Свободное движение рулевой поверхности после прекращения действия

внешней нагрузки

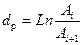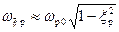; ; ; ; ; где- эквивалентная жёсткость - коэффициент вязкого трения всей конструкции

Рис.3.3

(3.1)

На практике C_пр приближённо может быть определена по известному моменту инерции рулевой поверхности и частоте собственных колебаний руля (если оценка ее известна). Приведем некоторые приближенные оценки параметров m_н, C_пр, h_н, на основании момента инерции руля J_р, логарифмического декремента затухания рулевой поверхности d_р и собственной частоты конструкции выходной части системы управления – рулевой поверхности и механической связи с приводом w_р:

,

где r_к – радиус качалки шарнирного соединения выходного звена привода (см. рис.3.1);

Орган управления полетом (рулевая поверхность или сопло ракетного двигателя) представляется некоторым инерционным объектом с массой m_н и собственным демпфированием h_н. Общие структурные свойства указанных рулевых приводов (привода массивной рулевой поверхности или привода ракетного двигателя) аналогичны и характеризуются следующими основными особенностями:

· Относительно низкая собственная частота выходной части привода w₀,

· Декремент затухания выходной части привода часто составляет d_р = 0,05¸0,2;

· Высокое быстродействие предварительных каскадов усиления управляющих сигналов, определяемое частотой среза электрогидравличеcкого усилителя (ЭГУ) мощности w_эгу >> w₀ [3.1].

Практика показывает, что удовлетворительная степень устойчивости таких приводов без дополнительных устройств коррекции может быть достигнута только при сравнительно низких значениях добротности позиционного контура К _д. Однако добротность позиционного контура определяет такие важные показатели привода, как быстродействие, динамическая точность и жесткость. Поэтому естественно стремление разработчика системы управления спроектировать привод с достаточно высокой добротностью.

В основе математического описания динамики электрогидравлического привода с дроссельным регулированием скорости, управляющим положением инерционного объекта (рулевой поверхности, сопла реактивного двигателя и т.п.), лежат уравнения баланса потоков рабочей жидкости на выходе золотникового гидрораспределителя и в гидроцилиндре, а также уравнения движения системы поршня с инерционным объектом. Характерной особенностью дальнейшего изложения динамики рулевого электрогидравлического привода является учёт в уравнениях жёсткости узлов крепления корпуса привода на летательном аппарате (Соп), а также же жёсткости связи поршня с центром масс объекта управления (Спр).

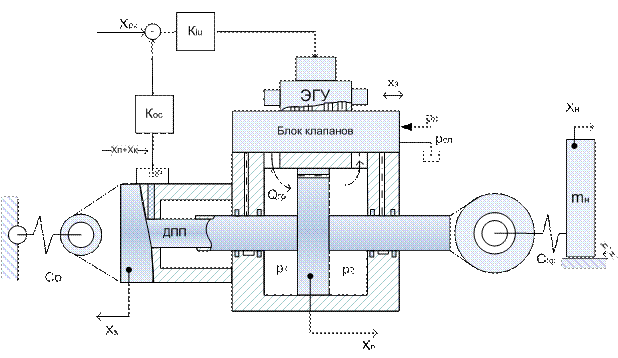
Рис. 3.4

Упрощённая схема электрогидравлического рулевого привода с учётом жёсткости узла крепления корпуса привода на самолёте (Со) и жёсткости конструкции связи поршня гидроцилиндра с центром масс инерционного объекта - рулевой поверхности (Спр).

Здесь: m_н – приведенная масса инерционного объекта; Кiu – коэффициент усиления электронного усилителя; Хк – перемещение корпуса привода; Х_п – перемещение поршня; Хн – перемещение центра масс; ДПП – датчик поступательных перемещений поршня; Qгр – расход жидкости на выходе ЭГУ; р1, р2 – давление в полостях гидроцилиндра.h_н – коэффициент вязкого трения; хз – перемещение золотника гидрораспределителя.

Уравнения баланса потоков рабочей жидкости в системе "гидрораспределитель – гидроцилиндр" в предположении ее симметричности имеют следующий вид:

, (4.3.2)

где Q_гр1, Q_гр2 – объемные расходы рабочей жидкости через рабочие окна гидрораспределителя в полость гидроцилиндра и из полости гидроцилиндра;

Q _v – расход, соответствующий скорости движения поршня относительно гидроцилиндра;

Q_сж – расход, соответствующий компенсации сжатия или расширения рабочей жидкости в полостях гидроцилиндра;

Q_ут – эквивалентный расход утечек рабочей жидкости через поршень гидроцилиндра.

Этот расход может быть обусловлен наличием специального канала кольцевания полостей гидроцилиндра или утечками через зазоры в гидрораспределителе или в уплотнительных узлах. Составляющие уравнений баланса потоков могут быть выражены следующим образом:

;

;

; (3.3)

; ;

,

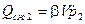где G_н1 (x_з), G_с (x_з) – зависимости проводимостей наливного и сливного рабочих окон золотника от его смещения (x_з);

А_п – эффективная площадь поршня гидроцилиндра;

b – эквивалентный коэффициент сжимаемости рабочей жидкости в гидроцилиндре;

k_ут – коэффициент линеаризованной зависимости расхода утечек в гидроцилиндре от перепада давления на поршне;

p_п, p_сл – давления подачи и слива;

p₁, p₂ – давления в полостях гидроцилиндра;

x_п, x_к – координаты смещения поршня и корпуса гидроцилиндра;

V – половина объема гидроцилиндра.

Уравнения движения инерционного объекта, корпуса привода и поршня гидроцилиндра в предположении малой инерционности двух последних элементов имеют вид

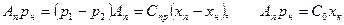; (3.4)

,

где x_н – перемещение инерционного объекта рулевой поверхности.

При появлении внешней силы, действующей на поршень, необходимо учитывать также жесткость гидроцилиндра (Сгц), определяемую, как сумма двух составляющих жесткостей: правой и левой полостей (Рис.4.3.6).

Функции, описывавшие расходы рабочей жидкости через гидрораспределитель в области малых воздействий x_з и отклонений p₁, p₂ в линейном приближении представляются в виде

; (3.5)

.

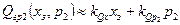Рис. 3.5

Схема замещения гидроцилиндра:

и 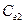- эквивалентные жесткости левой и правой полостей гидроцилиндра;

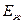- объемный модуль упругости рабочей жидкости; 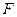- сила, действующая на поршень.

Геометрический и физический смысл коэффициентов линеаризации , ясен из рис.3.6, где а – регулировочная; б – силовая и в – обобщенные механические характеристики.

Рис. 3.7

Графическая интерпретация коэффициентов линеаризации в уравнениях баланса потоков рабочей жидкости в ветвях гидрораспределителя и гидроцилиндра (Q1, Q2). Здесь по горизонтальной оси отложено безразмерное давление в долях от давления подачи; KQp1 и KQp2 – коэффициенты линеаризации.

Рис.3.7

Дата добавления: 2014-01-07