Понятие о частоте среза электрогидравлического усилителя мощности

Динамические свойства электрогидравлических усилителей мощности (ЭГУ) в фирменных каталогах и проспектах представляются в виде оценки частоты, на которой фазочастотная характеристика пересекает уровень φ =-90º. Эта частота называется частотой пропускания электрогидравлического усилителя мощности. При этом приближённо основные наиболее существенные динамические свойства ЭГУ описываются в виде колебательного звена:

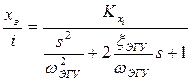, (3.5)

где: - частота среза ЭГУ, она соответствует частоте, на которой сдвиг по фазе ЭГУ достигает -90°(рис.3.7).

Для простоты рассуждений и наглядности оценок предположим, что частота среза электронного усилителя электрических сигналов w_эу и электрогидравлического усилителя мощности w_эгу много больше собственной частоты выходной части привода w₀, т.е. предположим, что выполняются следующие неравенства 3* w₀ << w_эгу, w₀ << w_эy, (4.3.6)

Здесь - собственная частота исполнительного механизма привода с инерционным объектом, а Сэ - эквивалентная жёсткость исполнительного механизма:

. (3.7)

Будем полагать, что расход на выходе ЭГУ Q_эгу = Qгр, т.е. расходу на выходе гидрораспределителя; Обозначим k_Qi – коэффициент усиления по расходу ЭГУ на холостом ходу: k_Qi = k_Qxk_xi, k_xi – коэффициент передачи электрогидравлического усилителя по перемещению золотника - .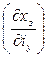

В современных высококачественных ЭГУ с 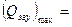45¸75 л/мин частота среза ЭГУ составляет w_эгу > 300 1/с, а x_эгу» 0,7. В двухкаскадных ЭГУ с 100 л/мин частота уменьшается до w_эгу < 120¸150 1/с.

Практика показывает, что для рулевых поверхностей современных самолетов собственная частота выходной части привода с инерционным объектом с учетом упругости конструкции составляет w₀ =36–120 1/с. Поэтому, для большинства рулевых приводов самолетов и тяжелых ракет, справедливо соотношение w_эгу > 3w₀. Таким образом, для приближенных оценок устойчивости рулевого привода на ранних этапах проектирования можно пренебречь инерционностью предварительных каскадов усиления сигналов и ЭГУ.

Рассмотрим систему дифференциальных уравнений описывающих динамику рулевого привода без учёта аэродинамической нагрузки (шарнирного момента), но с учётом указанных выше упругостей в конструкции привода.

С учетом сделанных допущений уравнения, описывающие основные динамические свойства указанных рулевых приводов, имеют следующий вид:

уравнение электрогидравлического и электронного усилителей

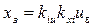, (3.8)

где k_iu, k_xi – коэффициенты усиления электронного усилителя и первого каскада электрогидравлического усилителя мощности;

u_e – сигнал рассогласования в прямой цепи привода на входе в электронный усилитель.

Выражение для сигнала рассогласования рулевого привода можно представить в следующем виде:

, (3.9)

где k_вх, k_ос – коэффициенты входа и обратной связи.

Выразим перемещение корпуса гидроцилиндра и скорость перемещения корпуса гидроцилиндра через давление нагрузки:

; (3.10)

Сила, развиваемая гидроцилиндром Fн привода, определяется выражением:

(3.11)

Здесь mн – приведенная к поршню масса объекта управления,

hн – коэффициент эквивалентного вязкого трения объекта.

Сила, развиваемая поршнем гидроцилиндра, создаётся перепадом давления в полостях гидроцилиндра. Перепад давления на поршне обозначается, как

Рн=Р1-Р2,

и называется давлением нагрузки. В этом случае уравнение (3.11) можно записать в следующем виде:

(3.12)

Выразим соотношения, которые связывают деформацию конструкции системы «поршень – центр масс инерционного объекта» (Хп-Хн) через давление нагрузки

Рн и перемещение инерционного объекта.

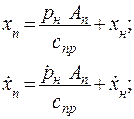(3.13)

Подставим полученные выражения в уравнения баланса потоков рабочей жидкости в магистралях ЭГУ и гидроцилиндра:

(3.14)

Приведя подобные члены, уравнение (4.3.14) представится в следующим виде:

(3.15)

Нетрудно видеть, что множитель (в квадратных скобках) перед есть не что иное, как эквивалентная жёсткость конструкции привода с учётом жёсткости гидроцилиндра (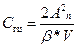) и жёсткости конструкции узлов установки привода на изделии (Со и Спр).

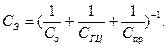(3.16)

Здесь 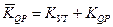- эквивалентный коэффициент наклона механической характеристики гидрораспределителя, который определяется наклоном параболы механической характеристики и влиянием коэффициента утечек рабочей жидкости из полости в полость гидроцилиндра (рис.3.7).

Дифференциальное уравнение баланса потоков рабочей жидкости в ветвях гидрораспределителя и в полостях гидроцилиндра привода, преобразованное относительно давления нагрузки Рн имеет следующий вид:

, (3.17)

где добротность следящего привода: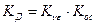

Кve – коэффициент усиления прямой цепи привода по скорости: Kve= ΔV/ΔUe.

Здесь ΔV - приращение скорости поршня при изменении сигнала рассогласования ΔUe. Обозначим - эквивалентную жесткость узлов конструкции установки привода на изделии: .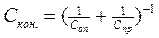

Нас интересует, в первую очередь, движение выходного звена при поступлении на вход привода управляющего сигнала. Поэтому, подставив в уравнение (3.17) выражение для давления нагрузки Рн (4.3.12), можно получить уравнение динамики привода при внешнем управляющем сигнале и при отсутствии внешнего силового воздействия, а также передаточную функцию рулевого привода с выходной координатой – перемещение инерционного объекта, центра масс рулевой поверхности:

(3.18)

. (3.19)

Для большинства проектных случаев в этом выражении ∆ << 1. Эта величина определяется следующим выражением: .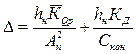

ξо - коэффициент относительного демпфирования привода с учетом упругости его узлов крепления на самолёте.

Демпфирование привода содержит три составляющих и определяется следующим выражением:

(3.20)

• Первое слагаемое определяется силами трения в системе подвижности системы привода.
• Второе слагаемое определяется утечками и наклоном механической характеристики .
• Третье слагаемое появилось из-за наличия упругости узлов крепления.

Последнее слагаемое определяет новые факторы влияния на демпфирование привода, которые определяются упругостью конструкции узлов крепления: с увеличением добротности позиционного контура привода демпфирование увеличивается, также как и с уменьшением жёсткости конструкции.

По полученной передаточной функции сделаем некоторые выводы и оценим влияние параметров на динамику следящих гидроприводов.

Для обеспечения устойчивости рулевого привода в соответствии с критерием Найквиста модуль передаточной функции разомкнутой системы на частоте, которая соответствует 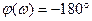должен быть меньше единицы. При сделанных нами ранее допущениях о быстродействии электронного усилителя и электрогидравлического усилителя мощности (ЭГУ) их динамику можно не учитывать. В этом случае фазочастотная характеристика разомкнутого привода всегда пересекает линию -180 градусов на частоте ω ₀ т.е. .

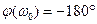В этом случае условие устойчивости рулевого привода примет следующий вид:

, при 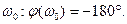, (3.21)

где 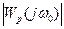- модуль частотной передаточной функции разомкнутой системы привода на собственной частоте.

Таким образом, условие устойчивости привода по Найквисту при выполнении условия имеет вид:

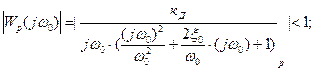(3.22)

преобразуя это выражение, получим условие устойчивости в следующем виде:

(3.23)

Откуда следует, что критическая добротность позиционного контура привода равна:

(3.24)

Возникает вопрос: можно ли за счёт 3-го слагаемого в выражении (4.3.20), уменьшая жёсткость конструкции узлов крепления привода Сконст., увеличить его устойчивость? Ведь с уменьшением этой жёсткости показатель демпфирования привода увеличивается! Предположим, что единственным источником демпфирования является Сконст., т.е.

В этом случае условие устойчивости привода на основании выражения (3.23) можно представить следующим образом:

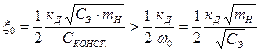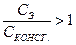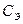
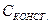Но это неравенство никогда не может быть выполнено, т. к. не может быть больше, чем. Таким образом, снижением жесткости узлов крепления привода нельзя увеличить его устойчивость.

Показатель демпфирования, определяемый трением, в основном определяется трением в подшипниках, конструкционным трением и вязким трением в уплотнениях гидроцилиндра, если оно есть. Этот показатель обычно лежит в следующих пределах:

Поэтому рабочая добротность привода при отсутствии специального канала перетечек может быть не больше чем

(3.25)

Окончательную проверку степени затухания переходного процесса, с учетом сухого трения в гидроцилиндре, необходимо выполнять методом математического моделирования.

Передаточная функция, определяющая движение перемещение поршня по отношению к входному сигналу.

Эту передаточную функцию определим в виде следующего отношения .

Выразим координату выходного звена привода – перемещение поршня через давление нагрузки (Рн) и перемещение центра масс инерционного объекта (Хн)

;

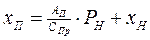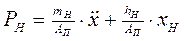; (3.26)

.

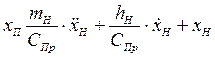Переходя к операторной форме получаем промежуточную передаточную функцию, связывающую перемещение центра масс инерционного объекта по отношению к перемещению поршня:

(3.27)

Демпфирование и собственная частота такой механической системы определяются выражениями:

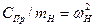и , (3.28)

здесь - собственная частота выходной части системы привода (собственная частота рулевой поверхности с учётом упругости конструкции связи руля с поршнем.

Структурная схема системы привода в этом случае примет следующий вид:

Рис.3.9

Структурная схема привода для оценки координаты перемещения поршня гидроцилиндра.

Общая передаточная функция, описывающая динамику системы привода с выходной координатой в виде перемещения поршня (Хп), может быть записана в следующей форме:

(3.29)

Типовой переходный процесс рулевого привода, управляющего положением инерционного объекта, показан на рис.3.10.

На рис.3.11 показаны типовые амплитудно-частотная характеристика и фазочастотная характеристики привода, полученные по передаточной функции, характеризующей перемещение центра масс инерционного объекта (Хн), так как именно эта координата характеризует эффективность управления объектом. На этом рисунке нанесены также границы, определяющие допустимые области расположения этих характеристик.

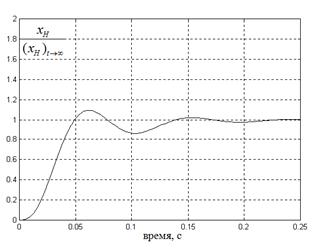Рис.3.10 Переходный процесс перемещения центра масс инерционного объекта рулевым приводом при ступенчатом сигнале управления при единичном коэффициенте передачи.

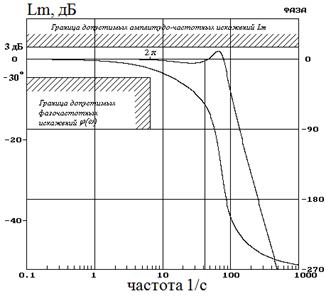Рис.3.11 Амплитуднофазочастотные характеристики рулевого привода. Штриховкой показаны типовые разрешённые области протекания кривых, которые задаются в техническом задании на проектирование рулевого привода.

Тема 4. Синтез оптимальных параметров привода с большой инерционной нагрузкой по интегральным критериям качества на плоскости обобщённых коэффициентов.

Представление динамики электрогидравлического рулевого привода на плоскости обобщённых коэффициентов и определение

Дата добавления: 2014-01-07