Регулятор состояния с измеряемыми координатами рулевого привода

Взаимосвязь между входным воздействием и выходными координатами привода, описываемые дифференциальным уравнение n -ого порядка, может быть представлено в виде n дифференциальных уравнений i -ого порядка для каждой из n координат, называемых координатами состояния. Координаты состояния могут быть любые, но не должны быть линейно зависимыми. Другими словами одна любая координата состояния не может выражаться через другую координату с помощью линейной операции. Например, если в качестве координаты состояния выбрано ускорение объекта управления, то перепад давления на поршне (давление нагрузки) не может быть выбран в качестве другой координаты состояния, т.к. они линейно зависимы.

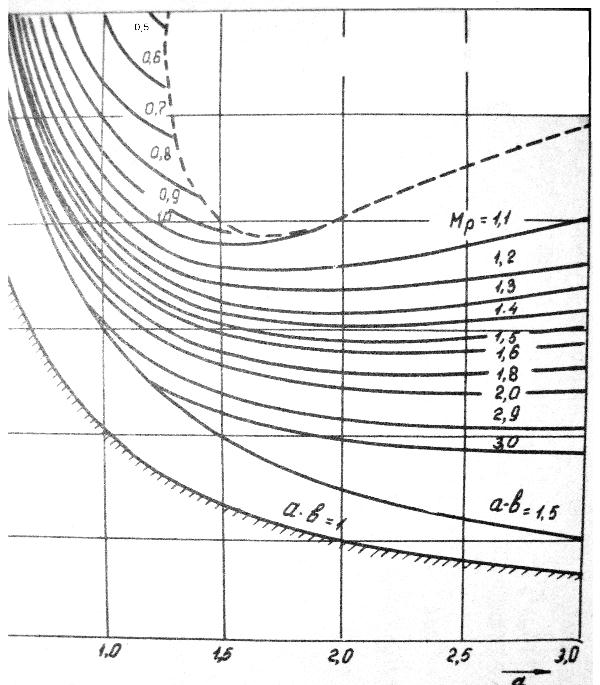
Рис.5.1

Максимум подъёма амплитудно-частотной характеристики рулевого привода в зависимости от параметров его передаточной функции

Предположим, что все координаты состояния могут быть измерены с помощью специальных датчиков, т.е. будут наблюдаемыми. Выберем в качестве координат состояния следующие координаты:

,

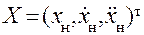т.е. перемещение объекта, его скорость и ускорение. Введём комплекс обратных связей по указанным координатам состояния, снимая сигналы с соответствующих датчиков. Построим схему управления приводом так, как это показано на рис.4.4.5. Совокупность обратных связей по всем координатам состояния образует регулятор состояния рулевого привода. Получим передаточную функцию следящего привода с указанным комплексом обратных связей, т.е. рулевого привода с регулятором состояния. Для этого будем последовательно замыкать по одной обратной связи, начиная с обратной связи по ускорению объекта. Таким образом, мы получим передаточную функцию рулевого привода с регулятором состояния, в который входит обратная связь по положению объекта, скорости, ускорению выходного звена.

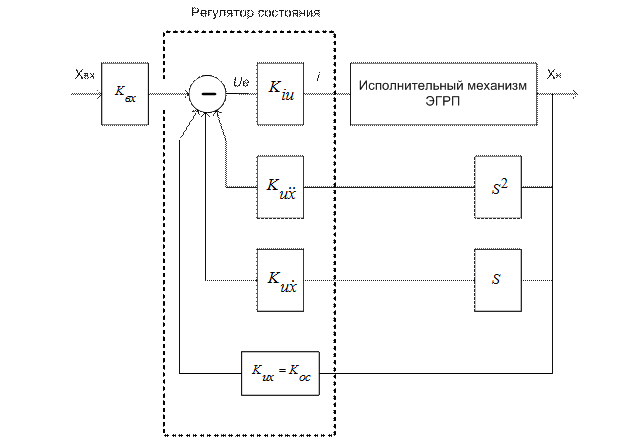Рис.5.2

Структурная схема рулевого электрогидравлического привода с регулятором состояния.

Здесь приняты следующие обозначения: Хвх – сигнал управления; Ue –сигнал рассогласования; I – ток в обмотке управления ЭГУ; Кос – коэффициент позиционной обратной связи (коэффициент по первой координате состояния).

Передаточная функция представленного выше регулятора имеет следующий вид:

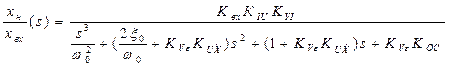(5.1)

В этом выражении приняты следующие обозначения:

К_вх - масштабный коэффициент входа (чаще всего он равен единице).

К_iu – коэффициент усиления электрических сигналов пред ЭГУ.

К_vi - коэффициент усиления по скорости рулевого агрегата Кvi=(Vmax/Imax)

K_ve – коэффициент усиления прямой цепи по скорости Kve= Кvi* Кiu.

Отметим, что произведение Kve*Кос=К_Д – добротность позиционного контура рулевого привода.

Уравнение регулятора состояния привода имеет вид

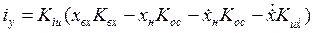. (5.2)

Проведём преобразования передаточной функции (4.4.10) и примем коэффициент передачи привода Квх/Кос=1. Если обозначить 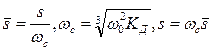, то получим следующую обобщенную передаточную функцию следящего привода:

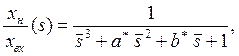(5.3)

которая характеризует динамические свойства рулевого привода с регулятором состояния.

В этой передаточной функции коэффициенты а * и b * имеют следующий вид:

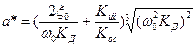
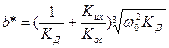(5.4)

Задаваясь желаемым расположением изображающей точки на плоскости обобщенных коэффициентов а * и b * можно определить требуемые коэффициенты обратных связей по ускорению и скорости выходной координаты привода следующим образом:

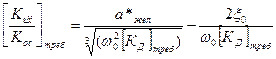, (5.5)

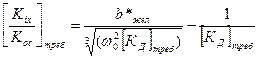. (5.6)

Значение добротности в большинстве практических случаев определяется из условия обеспечения фазочастотных характеристик привода на фиксированных частотах:

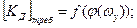
С точки зрения получения оптимальных переходных процессов в смысле минимума критерия ITAE можно воспользоваться соотношением

.

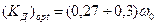Рассмотрим построение регулятора состояния с иным выбором координат состояния, а именно, выберем в качестве координат состояния положение выходного звена, его скорость и перепад давления на поршне, т.е. давление нагрузки. Вектор координат состояния примет вид:

.

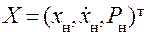Будем предполагать, что основная нагрузка привода, влияющая на его динамик при малых отклонениях координат – инерционная.

В этом случае схема рулевого привода с регулятором состояния примет вид, показанный на рис.5.3. Передаточная функция рулевого привода с данным регулятором состояния имеет следующий вид:

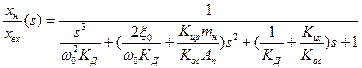(5.7)

Введем ранее использовавшуюся подстановку 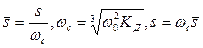в передаточную функцию привода, и получим обобщенную передаточную функцию следящего привода с регулятором состояния в следующем виде:

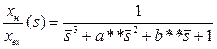(5.8)

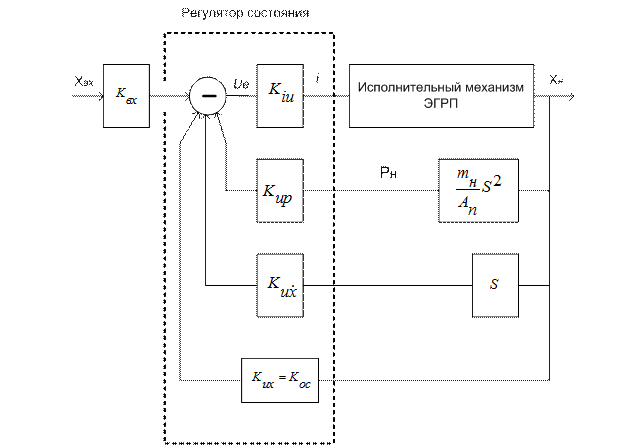
Рис.5.3

Структурная схема рулевого электрогидравлического привода с регулятором состояния. Здесь приняты следующие обозначения: Хвх – сигнал управления; Ue –сигнал рассогласования; I – ток в обмотке управления ЭГУ; Крн – коэффициент обратной связи по давлению нагрузки (перепаду давления на поршне).

В этой передаточной функции обобщенные коэффициенты а ** и b **, характеризующие динамику рулевого привода равны:

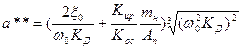(5.9)

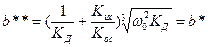
Имея в виду, что первый коэффициент а** характеризует демпфирование привода, по аналогии с предыдущими рассуждениями можно записать требуемый коэффициент обратной связи по давлению нагрузки Кup в следующей форме:

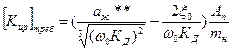. (5.10)

Здесь значение коэффициента а_ж** определяет желаемый уровень демпфирования привода. Его можно оценить по графикам, которые показаны на рис.4.2, 4.3, 5.1. Пусть на плоскости обобщённых коэффициентов при номинальных параметрах привода без регулятора динамика привода характеризуется точкой а_о и b_o (см. рис.5.4). При этих значениях параметров, как видно, привод неустойчив. Требуется путём соответствующего выбора коэффициентов 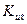(или Kve), 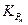перевести в положение, соответствующее желаемым динамическим свойствам, например в область минимума интегрального критерия ITAE, которая показана на этом же рисунке.

Для того чтоб реализовать регулятор состояния, который обеспечивал бы желаемые динамические свойства привода, система привода должна быть управляемой и наблюдаемой [5.1]. Напомним, что система называется управляемой, если все переменные состояния зависят от управляющего воздействия, то есть с помощью некоторого воздействия система из начального состояния переводится в другое. А для того, чтобы система была наблюдаемой- каждая из переменных должна быть связана с одним выходом (можно поставить датчик для измерения координаты).

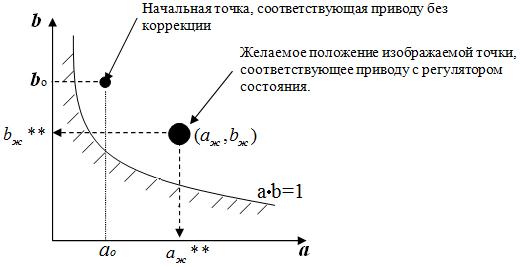
Рис.5.4

Дата добавления: 2014-01-07