Теплота сгорания

Задание состава окислителя

Задание состава горючих веществ

Литература

Содержание учебной дисциплины

Определение. Если переход системы из одного состояния в другое происходит скачком, а количество состояний системы (конечное или бесконечное) можно пронумеровать, то такая система называется системой дискретного типа.

Определение. процесс функционирования системы массового обслуживания называется случайным процессом.

Чтобы оптимизировать процесс функционирования системы массового обслуживания его надо изучить и описать математически.

Теория массового обслуживания является очень быстро развивающимся разделом теории вероятностей, т.к. ее применение на практике чрезвычайно широко.

Случайный процесс, протекающий в системе массового обслуживания состоит в том, что система в случайные моменты времени переходит из одного состояния в другое. Меняется число заявок, число занятых каналов, число заявок в очереди и проч.

Если количество возможных состояний счетно, то сумма вероятностей нахождения системы в одном из состояний равна 1.

Совокупность вероятностей p_k (t) для каждого момента времени характеризует данное сечение случайного процесса.

Случайные процессы со счетным множеством состояний бывают двух типов: c дискретным или непрерывным временем.

Если переходы системы из одного состояния в другое могут происходить только в строго определенные моменты времени, то случайный процесс будет процессом с дискретным временем, а если переход возможен в любой момент времени, то процесс будет процессом с непрерывным временем.

Поскольку в реальности заявки на систему массового обслуживания могут поступать в любой момент времени, то большинство реальных систем массового обслуживания будут системами с процессом с непрерывным временем.

Для того, чтобы описать случайный процесс в системе с непрерывным временем необходимо прежде всего проанализировать причины, вызывающие изменение состояния системы. Эти причины определяются потоком заявок, поступающих на систему.

Поток событий.

Определение. Потоком событий называется последовательность событий, происходящих один за другим в какие- то моменты времени.

Характер событий, образующих поток может быть различным, а если события отличаются друг от друга только моментом времени, в который они происходят, то такой поток событий называется однородным.

Однородный поток можно изобразить последовательностью точек на оси, соответствующей времени:

t₁ t₂ t_n

t

Определение. Поток событий называется регулярным, если события следует одно за другим через строго определенные промежутки времени.

Определение. Поток событий называется стационарным, если вероятность попадания того ли иного числа событий на участок времени t зависит только от длины участка и не зависит от того, где именно на оси расположен этот участок.

Стационарность потока событий означает, что плотность потока постоянна, отсутствуют промежутки времени, в течение которых событий больше чем обычно. Классический пример – “час пик” на транспорте.

Определение. Поток событий называется потоком без последействий, если для любых неперекрещивающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, опадающих на другие.

Отсутствие последействий означает, что заявки в систему поступают независимо друг от друга. Поток выходных событий систем массового обслуживания обычно имеет последействие, даже если входной поток его не имеет. Пример – вход пассажиров на станцию метро – поток без последействия, т.к. причины прихода отдельного пассажира не связаны с причинами прихода всех остальных, а выход пассажиров со станции – поток с последействием, т.к. он обусловлен прибытием поезда.

Последействие, свойственное выходному потоку следует учитывать, если этот поток в свою очередь является входным для какой- либо другой системы.

Определение. Поток событий называется ординарным, если вероятность попадания на элементарный участок D t двух или более событий достаточно мало по сравнению с вероятностью попадания одного события.

Условие ординарности означает, что заявки на систему приходят по одному, а не парами, тройками и т.д. Однако, если заявки поступают только парами, только тройками и т.д., то такой поток легко свести к ординарному.

Определение. Если поток событий стационарен, ординарен и без последействий, то такой поток называется простейшим (пуассоновским) потоком.

Это название связано с тем, что в этом случае число событий, попадающих на любой фиксированный интервал времени, распределено по распределению Пуассона.

В соответствии с этим законом распределения математическое ожидание числа точек, попавших попадающих на участок времени t, имеет вид:

l - плотность потока – среднее число событий в единицу времени.

Вероятность того, что за время t произойдет ровно т событий, равна

Вероятность того, что в течение данного времени не произойдет ни одного события, равна:

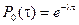
Пусть Т – промежуток времени между двумя произвольными соседними событиями в простейшем потоке. Найдем функцию распределения

В соответствии с законом распределения Пуассона, получаем:

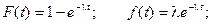
Математическое ожидание, дисперсия и среднее квадратическое отклонение этой величины соответственно равны:

Таким образом, для величины Т получили показательный закон распределения.

Пример. В бюро обслуживания в среднем поступает 12 заявок в час. Считая поток заказов простейшим, определить вероятность того, что: а) за 1 минуту не поступит ни одного заказа, б) за 10 минут поступит не более трех заказов.

Сначала найдем плотность (интенсивность) потока, выразив ее в количестве заявок в минуту. Очевидно, эта величина равна .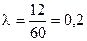

Далее находим вероятность того, что за время t = 1 мин не поступит ни одной заявки по формуле:

Вероятность того, что за 10 минут поступит не более трех заказов будет складываться из вероятностей того, что не поступит ни одного заказа, поступит один, два или ровно три заказа.

Пример. В ресторан прибывает в среднем 20 посетителей в час. Считая поток посетителей простейшим, и зная, что ресторан открывается в 11.00, определите:

а) вероятность того, что в 11.12 в ресторан придет 20 посетителей при условии, что в 11.07 их было 18

б) вероятность того, что между 11.28 и 11.30 в ресторане окажется новый посетитель, если известно, что предшествующий посетитель прибыл в 11.25.

Для ответ на первый вопрос фактически надо найти вероятность того, что в промежуток от 11.07 до 11.12 (t = 5 минут) придет ровно 2 посетителя. При этом мы знаем интенсивность потока посетителей - l = 20/60 = 1/3 посетителей в минуту. Конечно, данная величина носит условный характер, т.к. посетители не могут приходить по частям.

Искомая вероятность равна:

Теперь перейдем ко второму вопросу. Нам не сказано, сколько именно новых посетителей будет в промежутке от 11.28 до 11.30, главное чтобы был хоть один. Эта вероятность равна 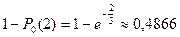. Здесь Р₀ (2) – вероятность того, что в этом промежутке не будет ни одного посетителя.

Если поток событий нестационарен, то его плотность l уже не является постоянной величиной, а зависит от времени.

Определение. Мгновенной плотностью потока событий называется предел отношения среднего числа событий, приходящегося на элементарный отрезок времени (t, t + Dt), к длине этого участка, которая стремиться к нулю.

Как видно из приведенного определения, с учетом того, что среднее число событий на участке времени равно математическому ожиданию, то можно сказать, что мгновенная плотность потока равна производной по времени от математического ожидания числа событий на участке (0, t).

Определение. Нестационарным пуассоновским потоком называется ординарный поток однородных событий без последействий с переменной плотностью l(t).

Для такого потока число событий, попадающих на участок длины t, начинающийся в точке t₀, подчиняется закону Пуассона:

Здесь а – математическое ожидание числа событий на участке от t₀ до t + t₀. Оно вычисляется по формуле:

Величина а на только от длины участка t, но и от его положения во времени. Закон распределения промежутка Т между двумя соседними событиями также будет зависеть от того, где на временной оси расположено первое из событий, а также от функции l(t).

Вероятность того, что на участке времени от t₀ до t + t₀ не появится ни одного события, равна

Тогда, соответственно, вероятность появления хотя бы одного события на этом интервале времени будет равна:

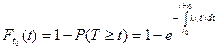
Плотность распределения можно найти дифференцированием:

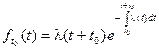
Эта плотность распределения уже не будет показательной. Она зависит от параметра t₀ и вида функции l(t). Однако, условие отсутствия последействия в этом виде потока сохраняется.

Поток Пальма.

Поток Пальма еще называют потоком с ограниченным последействием.

Определение. Потоком Пальма называется ординарный поток однородных событий, если промежутки между событиями Т₁, Т₂, … представляют собой независимые случайные величины.

Если промежутки времени Т₁, Т₂, … распределены по показательному закону, то поток Пальма становится простейшим потоком.

Примером потока Пальма может служить движение колонны автомобилей. Пусть движется колонна автомобилей, каждый из которых, двигаясь с одинаковой скоростью, стремится держаться на некотором заданном расстоянии от впереди идущего автомобиля. Однако, вследствие воздействия множества случайных факторов, это расстояние выдерживается не точно. Тогда времена пересечения каждым автомобилем определенного рубежа Т₁, Т₂, … будут независимыми случайными величинами и образуют по ток Пальма.

Отметим, что если автомобили будут стремиться выдерживать заданное расстояние не от соседней машины, а от головной, то моменты пересечения этого рубежа уже не будут образовывать поток Пальма.

Поток Пальма часто получается в качестве выходного потока систем массового обслуживания.

Теорема. (Теорема Пальма) Пусть на систему массового обслуживания поступает поток заявок типа Пальма, причем заявка, заставшая все каналы занятыми, получает отказ (не обслуживается). Если при этом время обслуживания имеет показательный закон распределения, то поток не обслуженных заявок является также потоком типа Пальма.

Этот факт важен, так как на практике получившие отказ заявки обычно перенаправляются на другую систему массового обслуживания, т.е. образуют для этой системы входной поток.

Так, если на систему массового обслуживания поступает простейший входной поток, то поток заявок, получивших отказ, уже не будет простейшим, однако, будет потоком с ограниченным последействием.

Потоки Эрланга.

Потоки Эрланга также являются потоками с ограниченным последействием. Они образуются просеиванием простейшего потока.

Суть этого просеивания состоит в следующем. Если изобразить на временной оси простейший поток, поставив в соответствие каждому событию некоторую точку, и выбросить из потока каждую вторую точку, то получим поток Эрланга первого порядка. Оставив каждую третью точку и выбросив две промежуточные, получаем поток Эрланга второго порядка и т.д.

Определение. Потоком Эрланга k – порядка называется поток, получаемый из простейшего, если сохранить в простейшем потоке каждую (k + 1) – ю точку, а остальные выбросить.

Очевидно, что простейший поток может рассматриваться как поток Эрланга нулевого порядка.

Пусть имеется простейший поток с интервалами Т₁, Т₂, … между событиями. Величина Т – промежуток времени между двумя соседними событиями в потоке Эрланга k – го порядка.

Очевидно, что . Так как первоначальный поток – простейший, то случайные величины Т₁, Т₂, … распределены по показательному закону:

Обозначим f_k(t) плотность распределения величины Т для потока Эрланга k – го порядка. Если умножить эту плотность на элементарный отрезок времени dt, мы получим вероятность того, что величина Т примет значение в некоторой сколь угодно малой окрестности точки t- (t, t + dt). На этот участок должна попасть конечная точка промежутка, а предыдущие k точек простейшего потока – на промежуток (0, t).

Вероятность первого события равна , а второго - . Эти события должны осуществиться совместно, значит, их вероятности надо перемножить.

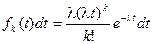
Полученный закон распределения называется законом распределением Эрланга k - го порядка.

При k = 0 получаем показательный закон распределения.

Математическое ожидание, дисперсия и среднее квадратическое отклонение для распределения Эрланга находятся по формулам:

Плотность потока Эрланга равна

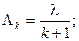
Для промежутка времени между двумя соседними событиями в потоке Т рассмотрим нормированную величину 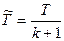. Такой поток будет называться нормированным потоком Эрланга.

Закон распределения для такого потока будет иметь вид:

,

Математическое ожидание и дисперсия будут равны:

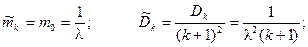
Получается, что неограниченном увеличении k нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными .

Изменение порядка нормированного потока Эрланга позволяет получить различную степень последействия. Последействие возрастает с увеличением k.

На практике это удобно для приближенного представления реального потока с каким – либо последействием потоком Эрланга. При этом порядок этого потока определяется из того соображения, чтобы характеристики потока Эрланга (математическое ожидание и дисперсия) совпадали с характеристиками исходного потока.

Цепи Маркова.

(Андрей Андреевич Марков (1856-1922) – русский математик, академик)

Определение. Процесс, протекающий в физической системе, называется марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.

Определение. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий A_i из полной группы. При этом условная вероятность p_ij(s) того, что в s –ом испытании наступит событие A_j при условии, что в (s – 1) – ом испытании наступило событие A_i, не зависит от результатов предшествующих испытаний.

Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями состояний системы.

По характеру изменений состояний цепи Маркова можно разделить на две группы.

Определение. Цепью Маркова с дискретным временем называется цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временем называется цепь, изменение состояний которой возможно в любые случайные моменты времени.

Определение. Однородной называется цепь Маркова, если условная вероятность p_ij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность p_ij называется переходной вероятностью.

Допустим, число состояний конечно и равно k.

Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:

Эта матрица называется матрицей перехода системы.

Т.к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то, очевидно, что сумма элементов каждой строки матрицы равна единице.

На основе матрицы перехода системы можно построить так называемый граф состояний системы,его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.

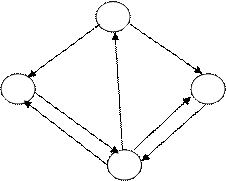
Пример. По заданной матрице перехода построить граф состояний.

Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.

S₁

0,2 0,7

S₂ 0,4 S₄

0,6 0,5

0,1 0,5

S₃

На графе не отмечаются вероятности перехода системы из одного состояния в то же самое. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.

Пусть P_ij(n) – вероятность того, что в результате n испытаний система перейдет из состояния i в состояние j, r – некоторое промежуточное состояние между состояниями i и j. Вероятности перехода из одного состояния в другое p_ij(1) = p_ij.

Тогда вероятность P_ij(n) может быть найдена по формуле, называемой равенством Маркова:

Здесь т – число шагов (испытаний), за которое система перешла из состояния i в состояние r.

В принципе, равенство Маркова есть ни что иное как несколько видоизменная формула полной вероятности.

Зная переходные вероятности (т.е. зная матрицу перехода Р₁), можно найти вероятности перехода из состояния в состояние за два шага P_ij(2), т.е. матрицу Р₂, зная ее – найти матрицу Р₃, и т.д.

Непосредственное применений полученной выше формулы не очень удобно, поэтому, можно воспользоваться приемами матричного исчисления (ведь эта формула по сути – не что иное как формула перемножения двух матриц).

Тогда в общем виде можно записать:

Вообще то этот факт обычно формулируется в виде теоремы, однако, ее доказательство достаточно простое, поэтому приводить его не буду.

Пример. Задана матрица переходов Р₁. Найти матрицу Р₃.

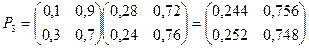
Определение. Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими. Если при некотором п все элементы матрицы Р^п не равны нулю, то такая матрица переходов называется регулярной.

Другими словами, регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через п шагов из любого состояния. Такие цепи Маркова также называются регулярными.

Теорема. (теорема о предельных вероятностях) Пусть дана регулярная цепь Маркова с п состояниями и Р – ее матрица вероятностей перехода. Тогда существует предел и матрица Р^(¥) имеет вид:

Т.е. матрица состоит из одинаковых строк.

Теперь о величинах u_i. Числа u₁, u₂, …, u_n называются предельными вероятностями. Эти вероятности не зависят от исходного состояния системы и являются компонентами собственного вектора матрицы Р^Т (транспонированной к матрице Р).

Этот вектор полностью определяется из условий:

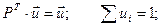
Пример. Найдем предельные вероятности для рассмотренного выше примера.

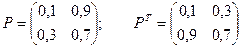
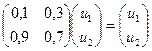
C учетом того, что u₁ + u₂ = 1, получаем:

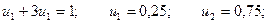
Получаем:

C:\temp4\lect1.DOC

Содежание КВМ Часть 1.

Содежание КВМ Часть 2.

Содержание КВМ Часть 3.

Содержание:

Теория вероятностей.

Основные понятия.

Операции над событиями.

Теорема сложения вероятностей.

Условная вероятность.

Теорема умножения вероятностей.

Формула полной вероятности.

Формула Бейеса.

Повторение испытаний. Формула Бернулли.

Случайные величины.

Закон распределения дискретной случайной величины.

Биноминальное распределение.

Распределение Пуассона.

Числовые характеристики дискретной случайной величины.

Математическое ожидание.

Свойства математического ожидания.

Дисперсия.

Вычисление дисперсии.

Свойства дисперсии.

Среднее квадратическое отклонение.

Функция распределения.

Свойства функции распределения.

Плотность распределения.

Свойства плотности распределения.

Числовые характеристики непрерывной случайной величины.

Равномерное распределение.

Показательное распределение.

Нормальный закон распределения.

Функция Лапласа.

Правило трех сигм.

Центральная предельная теорема Ляпунова.

Система случайных величин.

Плотность распределения системы двух случайных величин.

Условные законы распределения.

Условное математическое ожидание.

Зависимые и независимые случайные величины.

Линейная регрессия.

Линейная корреляция.

Закон больших чисел.

Неравенство Чебышева.

Теорема Чебышева.

Теорема Бернулли.

Предельные теоремы.

Характеристические функции.

Теория массового обслуживания.

Случайные процессы.

Поток событий.

Нестационарный пуассоновский поток.

Поток Пальма.

Потоки Эрланга.

Цепи Маркова.

Матрица переходов и граф состояний.

Предельные вероятности.

1. Лекции.

2. Практические занятия.

3. Заключительный контроль – экзамен

1. Частухин В.И., Частухин В.В. Топливо и теория горения: Учеб. пособие для вузов.– М.: Энергоатомиздат, 1990. – 224 с.

2. Чернов К.В. Источники энергии теплотехнологии Учеб. пособие.– Иваново, ИЭИ, 1991. – 128 с.

3. Драйздейл Д. Введение в динамику пожаров. М.: Стройиздат, 1990. – 424 с.

4. Розловский А.И. Основы техники взрывобезопасности при работе с горючими газами и парами. М.: Химия, 1980. – 376 с.

5. Процессы горения. / Абдурагимов И.М., Андросов А.С. и др. Под ред. Абдурагимова И.М. – М.: Изд-во ВИПТШ МВД СССР, 1984. – 270 с.

6. Хитрин Л.Н. Физика горения и взрыва. М.: МГУ,, 1957. – 452 с.

I. Закономерности горения техногенных веществ

1. Общая характеристика горения

1.1. Предварительные сведения

Горение в узком смысле представляет собой химическую реакцию соединения веществ с кислородом. Почти все вещества в той или иной степени подвержены окислению. Окисление с малой скоростью иногда называют медленным горением.

В широком смысле горением принято считать всякую быстропротекающую химическую реакцию, сопровождающуюся выделением тепла и света. С этой точки зрения вещества могут гореть не только в кислороде. Некоторые металлы горят в хлоре, окись натрия горит в углекислом газе, а порох горит без участия веществ окружающей среды.

Процесс горения является, прежде всего, химическим процессом, поскольку он сопровождается превращением вещества.

Развитие химического превращения не происходит обособленно. Химический процесс подчинён таким физическим процессам, как перенос тепловой энергии, диффузия. Кроме того, химическое превращение влечёт за собой перенос продуктов горения.

Всё это означает, что процесс горения в общем случае необходимо рассматривать как сложный физико-химический процесс, скорость которого определяется интенсивностью физических и химических явлений и особенностью их взаимовлияния.

1.2. Системнологический метод в теории горения

Системнология есть учение о целостности познания. Студент, достигший в своём интеллектуальном развитии определённого уровня, познаёт реальность целостно, т.е. системно.

Принципы построения познавательских систем имеют общий характер, их описание связано со следующими системнологическими понятиями: система, окружающая среда, компонент, связь.

Система – это часть реальности, извлечённая в процессе познания из более общей реальности, она состоит из компонентов, связанных в целое назначением системы.

Внутреннее пространство, содержащее компоненты, ограничено условной поверхностью, отделяющей систему от окружающей среды.

Свойства граничной поверхности определяют степень отличия системы от соответствующей ей реальности.

В зависимости от свойств ограничивающей поверхности система, по взаимодействию с окружающей средой, может быть:

– открытой,

– закрытой,

– изолированной,

– неизолированной и т.д.

Компонент есть функционально обособленная часть системы. Компонент представляет собой систему последующего уровня иерархии, которая вновь разделяется на компоненты следующего уровня и так далее, вплоть до элементарных компонентов, т.е. элементов системы.

Окружающая среда выражается особым компонентом системы, разделяемым на элементы в соответствии с назначением системы.

Все системы можно разделить на биогенные и абиогенные. Компонент абиогенной системы естественного происхождения представляет собой совокупность вещества и энергии.

В антропогенной системе при функционировании компонента может участвовать сциенция.

Связи в системе подразделяются на связи наследования свойств компонентов и связи межкомпонентного взаимодействия.

Связи наследования определяют прошлые и будущие состояния компонентов, а связи взаимодействия – нынешнее состояние системы.

В абиогенной системе естественного происхождения связи имеют вещественный и энергетический характер.

В антропогенной системе связи могут иметь сциентный характер.

Структура материальной системы представляет собой совокупность компонентов и связей взаимодействия между ними.

Человек, создающий описание познавательской системы, становится наблюдателем происходящих в ней событий, а также носителем времени.

Под событием следует понимать такое проявление связи наследования, которое приводит к изменению структуры системы.

Последовательности событий в компонентах и связях системы образуют процессы, например, процессы движения. Внутри системы происходят перемещения одних компонентов относительно других. Система признаётся движущейся, если все её компоненты перемещаются относительно окружающей среды.

Процессы в системе отражают закономерности материального мира.

1.3. Горючая система

Рассмотрим понятие «горючая система». Она предназначена для изучения закономерностей горения.

К основным компонентам горючей системы следует отнести горючее, окислитель и продукты горения. Дополнительными компонентами горючей системы могут быть:

– источник энергии, зажигающий горючее вещество;

– негорючее вещество, влияющее на условия горения.

Положение и свойства поверхности, ограничивающей горючую систему, в каждом случае должны оговариваться специально.

Окружающая среда для открытой системы служит источником и приёмником потоков вещества и энергии.

Горючим называется вещество, химически активные элементы которого при соединении с элементами окислителя способны окисляться.

Окислителем называется вещество, элементы которого при соединении с химически активными элементами горючего способны восстанавливються.

При окислительно‑восста­новительном соединении элементов горючего и окислителя образуются продукты горения.­ Под особыми условиями следует понимать соответствующие количественные соотношения между горючим и окислителем, а также необходимые термические условия.

К процессам, происходящим в горючей системе, относятся

– процессы переноса вещества и энергии,

– разложения сложных молекул на простые,

– пиролиза,

– испарения,

– плавления,

– ионизации,

– кинетики,

– образования продуктов горения,

– диссоциации и т.д.

Горючими веществами служат вещества, возникающие и обращающиеся в биосфере и антропосфере, а также техногенные вещества, создаваемые и применяемые в техносфере.

Горючие техногенные вещества, предназначенные для получения техногенной энергии, называются топливом.

При горении основным окислителем является кислород атмосферы.

Качественный и количественный состав продуктов горения зависит от условий в горючей системе.

Горючие техногенные вещества могут находиться в твёрдом, жидком и газообразном агрегатных состояниях. Окислитель – в жидком и газообразном.

Горючая система называется гетерогенной, если горючее и окислитель находятся в разных агрегатных состояниях, гомогенной, если – в одном, одинаковом, в газообразном или жидком состоянии.

Горючая система в зависимости от скорости движения может быть ламинарной или турбулентной. При малой скорости перемещения компонентов горючая система называется системой с ламинарным режимом движения, при большой – с турбулентным.

Горючая система в зависимости от соотношения физических и химических процессов может быть диффузионной или кинетической.

В диффузионной горючей системе определяющим является процесс взаимной диффузии горючего и окислителя, в кинетической – процесс химического реагирования между элементами горючего и окислителя.

В диффузионной системе воспламенение и сгорание сопровождается диффузией компонентов горения.

В кинетической системе горючее и окислитель предварительно перед горением перемешаны друг с другом до однородного состояния и диффузия не оказывает существенного влияния на интенсивность горения.

Горение как системнологическое понятие есть совокупность физико-химических процессов в горючей системе, возникающих и протекающих при специальных условиях, которые приводят к самоподдерживающемуся окислительно-восстановительному соединению элементов горючего и окислителя, сопровождающемуся возникновением продуктов горения, обнаруживаемых человеком через ощущения тепла и света или посредством измерений их показателей.

Горение в зависимости от вмешательства человека может быть организованным или неорганизованным. Организованное горение происходит в реакционном или топочном пространстве техногенных устройств. Неорганизованное горение протекает вне специальных устройств, оно составляет основу опасных природных, антропогенных или техногенных происшествий, называемых пожаром.

2. Состав и свойства горючих веществ

2.1.Классификация техногенных веществ, участвующих в горении

Техногенное вещество как системнологическое понятие есть вещество, применяемое или производимое в процессе техногенной деятельности.

Техногенное вещество, изучаемое в теории горения, может содержать в своём составе горючие и негорючие вещества. Исходные вещества по агрегатному состоянию подразделяются на следующие группы:

– газы,

– жидкости,

– твердые вещества.

Горючие газы представляют собой:

– простые газы, они состоят из однородных горючих молекул, которые содержат химически активные элементы;

– газовые смеси, они состоят из горючих и негорючих молекул;

– газовзвеси – это газовые смеси с распределёнными по объёму горючими и негорючими жидкими или твёрдыми частицами.

Горючие жидкости представляют собой:

– простые жидкости, они состоят из однородных горючих молекул, которые содержат химически активные элементы;

– жидкие смеси или растворы, они состоят из горючих и негорючих молекул;

– гидровзвеси – это жидкие смеси или растворы с распределёнными по объёму горючими и негорючими твёрдыми частицами;

– газожидкостные смеси – жидкие смеси с распределёнными по объёму горючими и негорючими газовыми включениями.

Горючие вещества в твёрдом состоянии представляют собой:

– твёрдые вещества простого состава – это простые аморфные или кристаллические вещества в твёрдом состоянии, состоящие из однородных горючих молекул или частиц, которые содержат химически активные элементы;

– твёрдые вещества сложного состава – это смеси и растворы, состоящие из горючих и негорючих молекул или частиц;

– твёрдые пористые вещества – это твёрдые вещества сложного состава с распределёнными по объёму слоя порами, заполненными горючими и негорючими газами;

– слой твёрдого вещества – это совокупность кусков твёрдого вещества сложного состава с промежутками, заполненными горючими и негорючими газами;

– аэрозоли – это частицы твёрдого вещества малого размера, взвешенные в воздушной среде.

Для расчёта горения необходимо знать состав горючих веществ. Этот состав обычно задаётся количеством одинаковых молекул или атомов вещества, выраженным их массой или объёмом от массы или объёма горючего в процентах.

В простом газе содержится 100 % горючего вещества, и он идентифицируется посредством химической формулы, отражающей структуру молекулы. Состав простого газа, включающего в себя, например, только молекулы водорода, можно представить:

а) в процентах по объёму

,%,об.

б) в объёмных долях

,

в) в процентах по массе

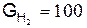,%,масс.

г) в массовых долях

.

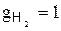Жидкие и твёрдые вещества простого состава количественно описываются аналогично.

В газовой смеси исходного состава содержатся горючие и негорючие молекулы. Они идентифицируется посредством соответствующих химических формул. Состав природного газа, включающего в себя метан, этан, азот, углекислый газ и водяной пар, можно представить:

а) в процентах по объёму

,%,

где – процентное содержание метана в природном газе исходного состава в объёмных единицах и т.д.;

б) в объёмных долях

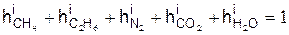
где – объёмная доля метана в природном газе исходного состава и т.д.;

в) в процентах по массе

,%,

– процентное содержание метана в природном газе исходного состава в массовых единицах и т.д.;

г) в массовых долях

,

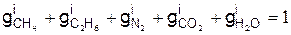где – массовая доля метана в природном газе и т.д.;

В обобщённом виде формулы для газовой смеси принимают вид

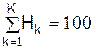,%, и т.д.

где k – номер молекулы в составе газовой смеси, K – количество молекул в газовой смеси.

При переходе от массовых единиц к объёмным пересчёт состава производится по формуле

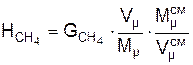
где V_m – молярный объём; M_m – молярная масса.

В газовой смеси исходного состава можно выделить сухую и горючую части. На примере природного газа сухой состав можно представить

а) сухим объёмом в процентах

,%,

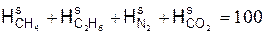где 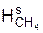– процентное содержание метана в сухом составе природного газа в объёмных единицах и т.д.;

б) сухими объёмными долями

,

где 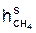– объёмная доля метана в природном газе сухого состава и т.д.;

в) сухой массой в процентах

,%,

где 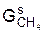– процентное содержание метана в сухом составе природного газа в массовых единицах и т.д.;

г) сухими массовыми долями

,

где – массовая доля метана в природном газе сухого состава и т.д.;

Горючий состав задаётся

а) горючим объёмом в процентах

,%,

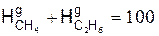где 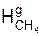– процентное содержание метана в горючем составе природного газа в объёмных единицах и т.д.;

б) горючими объёмными долями

,

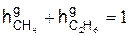где – объёмная доля метана в природном газе горючего состава и т.д.;

в) горючей массой в процентах

,%,

где – процентное содержание метана в горючем составе природного газа в массовых единицах и т.д.;

г) горючими массовыми долями

,

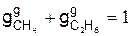где 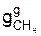– массовая доля метана в природном газе сухого состава и т.д.;

Объём вещества должен соответствовать определённым термическими условиями, определяющими его количество. Обычно количество вещества определяют для нормальных термических условий, при которых давление составляет 101,3 кПа, а температура – 273 К, иногда объём вещества приводят к стандартным термическим условиям: давление – 101,3 кПа, температура – 293 К.

Сложные по составу жидкие и твёрдые вещества, состоящие из молекул известной структуры, количественно описываются аналогично газовым смесям.

Сложные горючие вещества, состоящие из молекул, вид или количество которых неизвестны, описываются количеством атомов, входящих в молекулы. К числу атомов, определяющих структуру сложных техногенных веществ, относятся, прежде всего, углерод (C), водород (H), кислород (O), азот (N), сера (S), а также фтор (F), хлор (Cl), бром (Br) и другие.

В сложном горючем веществе можно выделить органическую сухую и горючую части; при пиролизе образуются летучие вещества и вещества твёрдого остатка.

Органический состав горючего вещества задаётся в процентах по массе суммой следующих элементов:

, %,

где – процентное содержание серы органических компонентов вещества.

Горючий состав горючего вещества задаётся в процентах по массе суммой следующих элементов

, %.

Сухой состав горючего вещества задаётся в процентах по массе суммой следующих компонентов

, %,

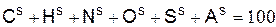где – процентное содержание негорючих компонентов, образующих после горения зольный остаток.

Исходный состав горючего вещества задаётся в процентах по массе суммой следующих компонентов

, %,

где Wⁱ – процентное содержание Н₂О в массе горючего вещества исходного состава.

Пересчёт количества компонента от одного состав к другомупроводится на основе закона сохранения вещества, например

,

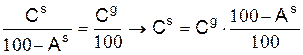для других компонентов и составов аналогично.

Основным окислителем при горении техногенных веществ является молекулярный кислород в несвязанном, т.е. в свободном состоянии. Кроме свободного кислорода окислителями могут быть вещества, содержащие в своём составе связанный кислород, к ним относятся: селитры (KNO₃); азотная кислота (HNO₃); перхлораты (вещества, содержащие в своём составе ClO₄, например KClO₄, NH₃ClO₄); окислы азота (NO₂, N₂O₅). К окислителям также относятся простые химические вещества – фтор, хлор, бром, взаимодействующие при горении с водородом. В дальнейшем будем исходить из того, что основным окислителем служит кислород воздуха.

В состав сухого воздуха, находящегося у поверхности Земли, входят:

§ азот – 78.084 %,

§ кислород – 20.946 %,

§ аргон – 0.934 %,

§ углекислый газ – 0.033 %,

§ неон, гелий, криптон, водород, ксенон, озон – всего в сумме 0.003%.

Содержание водяных паров во влажном воздухе переменно, их количество зависит от местности, времени года, климатических условий. и определяется температурой воздуха и атмосферным давлением.

Для расчётов горения обычно принимают следующий упрощенный состав воздуха: , .

Количество тепловой энергии, выделяемое при полном сгорании единицы горючего вещества, например 1 кг или 1 м³, называют теплотой сгорания – Q.

При сгорании горючего вещества, имеющаяся в нём влага нагревается до температуры кипения и испаряется, поглощая часть тепловой энергии, выделяемой при горении. В парообразном состоянии оказывается также вода, образующаяся в результате окисления компонентов горючего, содержащих водород.

Количество тепловой энергии, выделяемое при полном сгорании единицы горючего вещества, включая тепловую энергию конденсации образующиеся при этом водяных паров, называют высшей теплотой сгорания – Q_В. Количество тепловой энергии, выделяемое при полном сгорании единицы горючего вещества, за исключением тепловой энергии конденсации образующихся при этом водяных паров, называют низшей теплотой сгорания – Q_Н. Соотношение между высшей и низшей теплотами сгорания горючего вещества выражается формулой

,

где 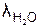– скрытая теплота конденсации водяного пара; – масса воды в продуктах горения, приходящаяся на единицу горючего вещества.

Дата добавления: 2014-01-07