Свойства одномерных ударных волн

Рассмотрим свойства стационарной ударной волны, представленной в виде плоского фронта, распространяющегося по инертному газу со скоростью D. Предположим, что свойства газа скачком изменяются на фронте, оставаясь постоянными в областях перед фронтом и за ним. Свойства газа припишем двум контрольным поверхностям, параллельным фронту. Схема распределения параметров газа относительно фронта имеет вид

Рис. 22. Схема распространения фронта

1-1 и 2-2 – контрольные поверхности

Поток газа, протекающего через контрольные поверхности, строго подчиняется законам сохранения массы, импульса и энергии.

При написании уравнений будем пользоваться относительными скоростями, т.е.

Для фронта волны в движущемся невязком, инертном газе справедливы следующие уравнения

а) закона сохранения массы

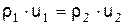, (1)

где r₁, r₂ – плотность газа до и после сжатия; D – скорость движения фронта волны; u₁ – скорость движения газа до сжатия относительно фронта; u₂ – скорость движения газа после сжатия относительно фронта;

б)закона сохранения импульса (количества движения)

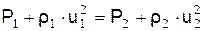, (2)

где Р₁ – давление газа перед фронтом волны; Р₂ – давление газа на фронте волны;

в)закона сохранения энергии

, (3)

где h = е + P/r – энтальпия; е – внутренняя энергия.

Давление и плотность газа связаны термическим уравнением состояния

. (4)

Соотношение (2) можно записать в следующем виде

,

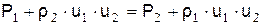отсюда

.

Если газ перед ударной волной неподвижен, то

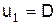
с учётом (1) получается формула для скорости распространения фронта волны

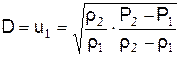. (5)

Исключение скорости из (1) – (3) приводит к выражению

,

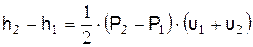или

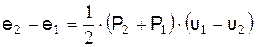(6)

где u – удельный объём.

Уравнение (6) называют уравнением адиабаты Гюгонио. Оно характеризует связь между начальным и конечным состояниями газа при заданном изменении энтальпии или энергии на ударном фронте. Это аналог соотношений, характеризующих адиабатические процессы.

На графике в координатах Р–u адиабата Гюгонио имеет следующий вид

Рис. 23. Адиабата Гюгонио

Линия Рu^k = const выражает собой все возможные состояния газа при адиабатическом сжатии, т.е. при сжатии без потерь энергии.

Допустим, что показатель адиабаты k не изменяется на ударном фронте. Комбинируя уравнения (1) – (4) можно выразить изменения давления, плотности и температуры на ударном фронте

,

,

,

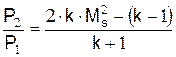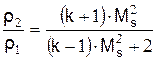где k – показатель адиабаты, М_s – число Маха

,

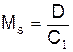где С₁ – скорость звука

.

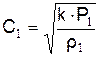Для того чтобы воспользоваться приведёнными соотношениями, нужно знать скорость фронта и начальные параметры газа.

Дата добавления: 2014-01-07