Квантование по уровню

Квантование по уровню – это процесс замены непрерывной функции ее отдельными значениями, отстоящими друг от друга на конечный интервал (уровень). При квантовании значение функции в произвольный момент времени заменяется ее ближайшим значением, называемым уровнем квантования. Интервал между двумя дискретными значениями уровней называется шагом квантования (q).

Рис. Квантование сигнала по уровню:

а – с постоянным шагом квантования; б – погрешности квантования; в – квантование с переменным шагом

По оси ординат откладывается величина заранее выбранного шага квантования q и проводятся линии, параллельные оси времени, обозначающие уровни квантования. Переход с одного уровня на другой происходит, когда значение функции находится в середине интервала квантования. Переход с одного уровня на другой происходит, когда значение функции находится в середине интервала квантования, так как в этот момент абсолютная погрешность квантование ∆ _к.у. оказывается наибольшей. Действительно, если значение функции находится в середине между двумя уровнями (точки а, б, в…), то возникает неопределенность, так как функция равноудалена от обоих уровней. Так, например, если значение функции в точке в возникает на бесконечно малую величину, то это новое значение целесообразно отнести к уровню 3. Наоборот, значение функции, несколько меньше значения в точки в, будет заменено уровнем 2. Исходя из сказанного процесс квантования осуществляется следующим образом: интервал квантования делится пополам, и проводится пунктирные горизонтальные линии до их пересечения с квантуемой функцией. Точки пересечения обозначаются буквами (а, b, c, d и т.д.), в них значение функции передается наименее точно, возникает ошибка квантования ∆ к.у., равная разности между значением функции λ(t) и ближайшим уровнем. Так как наименее точно функция передается в точке, находящейся между двумя уровнями квантования и отстоящей от них на половину интервала квантования q /2, то максимальная ошибка квантования по уровню определится как

(2.1)

Здесь + q /2 - максимальная положительная ошибка квантования, например, от точки в до уровня 2, а - q /2 – максимальная отрицательная ошибка квантования, например, от точки в до уровня 3. Погрешность квантования представлены на рис. б), на котором на оси времени отложены отрезки уровней квантования, пересекаемые функцией.

Так, функция между точками k и a пересекает уровень 2. Этот уровень отложен на оси t (рис. г.б), и проведен отрезок функции k-a. На участке а-b функция хотя и не пересекает ни один из уровней, но так как она проходит ближе к уровню 1, то отрезок этого уровня откладывается на оси времени. В этом диапазоне от точки а до точки b погрешность отсчитывается от уровня 1 и будет только положительная. На других участках имеет место погрешность и положительная, и отрицательная.

Таким образом, в результате квантования функции (t), произведенного по определенному правилу, был отобран ряд дискретных значений этой функции в точках а, b, c, d и т.д. Отбором точек и заканчивается собственно процесс квантования. Если же необходимо представить себе полностью форму той функции, которая заменила функцию (t), поступают следующим образом. Через точки а, b, c, d и т. д. проводят вертикальные отрезки (до их пересечения с уровнями), которые затем соединяются горизонтальными отрезками, образуя ступенчатую квантованную функцию 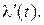Из рис. г), а) следует, что квантованная ступенчатая функция 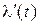как бы обходит с двух сторон (выше и ниже) непрерывную функцию это позволяет рассматривать квантование как результат положения на функцию помехи ∆(t), которую называют шумом или помехой квантования.

Как следует из рис. а), число уровней квантования N на единицу больше числа интервала N – 1.

Если сообщение 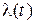ограничено диапазоном от 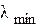до , то

.

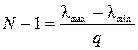При 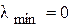имеем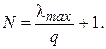

Что касается точности преобразования (квантования), то обычно она задается в виде значения приведенной относительной погрешности (в %), которая по определению равна 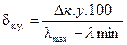. При описанном выше методе квантование (рис. б) погрешность не может превышать q /2, т.е. при подсчете нужно учитывать (2-1). Таким образом, считая, что 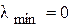(это достигается соответствующим расположением осей координат) получим

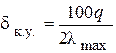(2-4)

и шаг квантования при заданной погрешности квантования равен

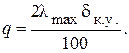(2-5)

Пример 2-1. Предположим, необходимо провести квантование непрерывной функции, от нуля до 100 В, с точностью 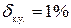. Согласно (2-5) q = 2В. Из (2-3) определяем, что необходим 51 уровень квантования.

Замена действительного значения функции ее ближайшим значением создает погрешность квантования, которая может принять любые величины от – q /2 до + q /2 (рис. б). При достаточно большом числе уровней квантование N распределение погрешности квантования в пределах от – q /2 до + q /2 будет равномерное независимо от закона распределения самой функции 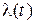. Средне – квадратичное значение погрешности квантования по уровню

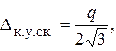
т. е. в 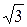раз меньше максимальной ошибки.

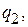
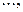
Неравномерное квантование по уровню. Некоторые функции, подлежащие квантованию, изменяются так, что их целесообразно квантовать с переменным шагом квантования Так, на рис. г) показана нелинейная зависимость тока I от напряжения U. Если необходимо при измерении получить равномерную шкалу напряжений, то отсчет по току надо вести с переменным шагом q, уменьшая его с ростом амплитуды. Могут быть и другие варианты изменения шага квантования. Так, например, если необходимо получить более точные значения в какой-либо части квантуемой функции, то в этом диапазоне шаг квантования следует уменьшить.

О восстановлении функции, квантованной по уровню. Квантование по уровню осуществляется для последующего кодирования, т.е. каждый уровень квантованной функции передается кодом.

На приемной стороне кодовая комбинация, поступая на дешифратор, преобразуется в ток или напряжения, которые используются по назначению (отклоняют стрелку прибора, изменяют показания цифровых индикаторов и т.д.). Принятая квантованная функция в своем первоначальном (непрерывном) виде на приеме обычно не восстанавливается, хотя это можно сделать путем линейной или более сложной интерполяции. Простейшая ступенчатая интерполяция функции 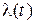была осуществлена, когда мы горизонтальными отрезками соединяли вертикальные отрезки, образуя функцию (рис. а).

Квантование по времени (дискретизация)

Если замена непрерывной функции её отдельными значениями производится в определенные моменты времени, то этот процесс называется квантованием по времени, или дискретизацией. На рис. а) показано, что горизонтальная ось времени делится на интервалы, отстоящие друг от друга на один и тот же интервал квантования .

Далее проводят вертикальные линии до пересечения с квантуемой функцией в точках 1, 2, 3,..., 9 и определяют значения функции, начиная с Это значит, что в интервале Т непрерывная функция 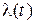будет передаваться не бесконечным рядом значений, а в данном случае всего лишь десятью значениями. Нахождение точек, определяющих значение непрерывной функции в дискретные моменты времени, как и в квантовании по уровню, собственно процесс квантование по времени и заканчивается.

В том случае, если желают восстановить квантованную функцию, осуществляют один из видов интерполяции, например, ступенчатую. При этом проводят из точек 0, 1, 2,..., 9 горизонтальные линии до пересечения их с вертикальными линиями, т.е. линии 0-1', 1- 2' и т.д. Далее точки 1'-1, 2'-2, 3'-3 и т.д. соединяют и получают ломаную квантованную функцию '(t).

Очевидно, что чем больше дискретных значений передается за время Т, т.е. чем меньше шаг квантования t, тем с большей точностью будет восстановлена на приеме функция 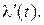Однако излишне малая величина t увеличивает массив измеренных значений и для их запоминания требуется больший объем памяти. В то же время при чрезмерно большом шаге квантования воспроизводимая функция будет не очень точной и сильно искаженной.

Рис. Квантование сообщения по времени:

а – метод квантования и восстановление функции ступенчатой интерполяцией; б – погрешности квантования; в – восстановление функции линейной интерполяцией

Шаг квантования можно определить из теоремы Котельникова, смысл которого заключается в следующим: любая непрерывная функция, спектр частот которой ограничен частотой F_макс, может быть полностью восстановлена по ее дискретным значением, взятым через интервалы времени

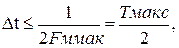
Однако имеется ряд ограничений для практичного применения этой теоремы. Так, все сообщения, передаваемые в телемеханике, ограничения во времени. Это обычно видео или радио импульсы длительностью τ, у которых согласно (1-14) и (1-22) спектр бесконечен. Поэтому представляет значительные трудности выбор величины F _макс в (2-7) для функции, ограниченных во времени. Так, например, если предавать синусоидальное напряжение с частотой в 50 Гц бесконечно долго во времени, то согласно (2-7) для восстановления его формы его формы на приеме достаточно передать за период лишь два импульса, соответствующих амплитудным значениям: один – положительной полуволне, другой – отрицательной. если же предавать синусоидальное напряжение в конечном отрезке времени, например, то для восстановления формы этого радиоимпульса необходимо уже не два, а значительно больше импульсов, хотя точно указать их число невозможно из – за того, что спектр частот радиоимпульсов бесконечен.

практически теореме Котельникова можно принять со следующей поправкой:

(2-8)

где η – коэффициент, зависящий от точности воспроизведения функции и способа интерполяции: при линейной η_л = 0,75/и при ступенчатой η_ст = (3-5)η_л (δ – относительная погрешность в %)

Существует и другой подход определения шага квантования, исходящий из задаваемой величины погрешности. для примера на рис. б) начерчены в виде фигур, близких к треугольникам, величины абсолютных погрешностей, возникающих при квантовании; эти фигуры подобны токовым же на рис. а). на рис. б) показано, что заданная величина абсолютной погрешности ∆₃ на одном участке нарастания функции λ(t) достигается за период ∆ t, на другом за ∆ t ₂, а на некоторых она оказывается меньше заданной (например, на участке 1` - 2`). Это зависит от скорости нарастания функции λ=dλ/d t. Очевидно, следует выбрать такой шаг квантования, который соответствует максимальной скорости нарастания функции 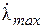. Так, из рис. а) следует, что если бы на участке кривой 5-6 имелся всплеск функции (пунктир), то выбранный шаг квантования t оказался бы излишне большим и этот всплеск не был бы восстановлен (следовало бы взять шаг ).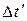

Из рис. б) видно, что

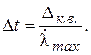(2-9)

Если считать, что максимальная скорость нарастания сохраняется во всем диапазоне изменения сообщения от нуля до максимального значения, то минимальное время изменения сообщения во всем диапазоне

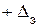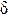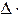Величина абсолютной погрешности показана на рис. б). Здесь, как и в квантовании по уровню, при расчетах следует учитывать или , или , т.е. в среднем /2. Это значит, что = 100/2. Подставляя отсюда значение в (2-9), а значение 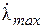из (2-11), получаем

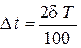. (2-11)

Формула выведена с учетом восстановления функции при помощи ступенчатой интерполяции.

Пример 2-2. Найти ∆ t при квантовании синусоидального напряжения частоты F = 50 Гц. Погрешности при восстановлении δ = 1%. Согласно (2-7) ∆ t = 1/2*50*10^-3 =10мм, т.е. в идеальном случае каждую полуволну синусоиды можно передавать лишь одним значением [период τ= 1/(50*10^-3 )=20мм]. η_л.и.=0,75/ 0,75/ = 7,5, то для ступенчатой интерполяции η_ст=25 и ∆ t _ст= 1/25*2*50*10^-3=0,4_мсек..Так же результат получается и из (2-11). Таким образом, при заданной точности восстановления, каждый полупериод синусоиды следует предавать одним значением, а примерно 25 при ступенчатой интерполяции и 7,5 при линейной.

Восстановить квантованную по времени функцию на приемной стороне можно при помощи ступенчатой или линейной интерполяции или используя метод Котельникова. Чаще всего применяется ступенчатая интерполяция, и наиболее редко используется фильтрация по Котельникову. Ступенчатая интерполяция на рис. а) выполняется с помощью запоминающих устройств, сохраняющих значения до появления следующего значения

Погрешность от ступенчатой интерполяции изображена на рис. б). Причем под погрешностью интерполяции понимается разность между мгновенными значениями восстановленного и исходного символов, взятых в одни и те же моменты времени. Максимальная погрешность возникает в точках 1', 2',..., 9'. Погрешность равна нулю в точках 1, 2, 3,..., 9. В общем случае задаются среднеквадратичные значения этой погрешности:

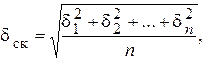
где n – число замеров.

При восстановлении квантованной функции по Котельникову нужно знать все дискретные точки, как предыдущие, так и последующие, или во всяком случае для практической реализации должно быть известно несколько точек до и после интервала, в котором происходит интерполяция. Знание последующих точек возможно, лишь в системах, допускающих запаздывание в передаче информации. Большинство телемеханических систем работает в реальном масштабе времени и не допускает запаздывания. В таких системах приходится использовать ступенчатую интерполяцию, так как для линейной, нужно знать наперед хотя бы одну точку, что опять требует запаздывания. Действительно, если, например, известно значение функции в момент t ₄ (рис. а), т. 4), то при ступенчатой интерполяции нам заранее известно, что через ∆t значение функции будет тем же (т. 5`). Каким оно будет при линейной интерполяции через интервал ∆ t, неизвестно: то ли значение возрастает (т. 5), то ли уменьшится (т. 5₂).

Иногда восстановление функции, квантованной по времени, с шагом, подсчитанным по теореме Котельникова, производится при помощи фильтра НЧ, который выделяет постоянную составляющую и низкочастотные составляющие, соответствующие спектру передаваемой функции. Однако при этом возникают погрешности из–за того, что амплитудно–частотная характеристика реального фильтра отличается от характеристики идеального фильтра. Восстановление при помощи фильтра имеет смысл, если спектр передаваемой функции достаточно сосредоточен в области нуля по оси частот. Зачастую квантование по времени используется для осуществления амплитудно – импульсной модуляции.

Дата добавления: 2014-01-07