Тема 4. Парная линейная регрессия. Метод наименьших квадратов

Коэффициент корреляции указывает на степень тесноты взаимосвязи между двумя признаками, но он не дает ответа на вопрос, как изменение одного признака на одну единицу его размерности влияет на изменение другого признака. Для того чтобы ответить на этот вопрос, пользуются методами регрессионного анализа.

Регрессионный анализ устанавливает форму зависимости между случайной величиной 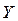и значениями переменной величины , причем, значения считаются точно заданными.

Уравнение регрессии – это формула статистической связи между переменными.

Если эта формула линейна, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией (нескольких переменных – множественной).

Выбор формулы зависимости называется спецификацией уравнения регрессии. Оценка значений параметров выбранной формулы называется параметризацией.

Как же оценить значения параметров и проверить надёжность сделанных оценок?

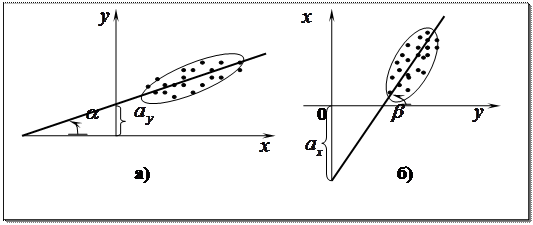
Рассмотрим рисунок

· На графике (а) взаимосвязь х и у близка к линейной, прямая линия 1 здесь близка к точкам наблюдений и последние отклоняются от неё лишь в результате сравнительно небольших случайных воздействий.

· На графике (б) реальная взаимосвязь величин х и у описывается нелинейной функцией 2, и какую бы мы ни провели прямую линию (например, 1), отклонения точек от неё будут неслучайными.

· На графике (в) взаимосвязь между переменными х и у отсутствует, и результаты параметризации любой формулы зависимости будут неудачными.

Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Всегда можно попытаться провести такую прямую линию, которая будет «ближайшей» к точкам наблюдений по их совокупности (например, на рисунке (в) лучшей будет прямая 1, чем прямая 2).

Теоретическое уравнение парной линейной регрессии имеет вид:

,

где 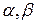называются теоретическими параметрами (теоретическими коэффициентами) регрессии; - случайным отклонением (случайной ошибкой).

В общем виде теоретическую модель будем представлять в виде:

.

Для определения значений теоретических коэффициентов регрессии необходимо знать все значения переменных Х и Y, т.е. всю генеральную совокупность, что практически невозможно.

Задача состоит в следующем: по имеющимся данным наблюдений 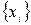, необходимо оценить значения параметров .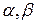

Пусть а – оценка параметра 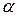, b – оценка параметра .

Тогда оценённое уравнение регрессии имеет вид: ,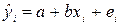

где теоретические значения зависимой переменной y, 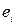- наблюдаемые значения ошибок . Это уравнение называется эмпирическим уравнением регрессии. Будем его записывать в виде .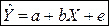

В основе оценки параметров линейной регрессии лежит Метод Наименьших Квадратов (МНК) – это метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.

.

Функция Q является квадратичной функцией двух параметров a и b. Т.к. она непрерывна, выпукла и ограничена снизу (), поэтому она достигает минимума. Необходимым условием существования минимума является равенство нулю её частных производных по a и b:

.

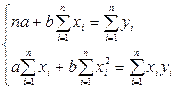Разделив оба уравнения системы на n, получим:

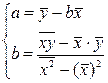или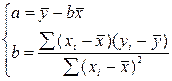

Иначе можно записать:

и - средние квадратические отклонения значений тех же признаков.

Т.о. линия регрессии проходит через точку со средними значениями х и у , а коэффициент регрессии b пропорционален показателю ковариации и коэффициенту линейной корреляции.

Если кроме регрессии Y на X для тех же эмпирических значений найдено уравнение регрессии X на Y (, где ), то произведение коэффициентов :

.

Коэффициент регрессии 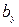- это величина, показывающая, на сколько единиц размерности изменится величина при изменении величины 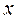на одну единицу ее размерности. Аналогично определяется коэффициент .

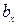Как и коэффициент корреляции, коэффициент регрессии может принимать и положительные и отрицательные значения. Например, если коэффициент 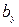имеет знак "-", то это означает, что при увеличении значения признака 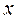на единицу его размерности значение признака 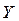уменьшается на величину, равную .

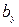Уравнения линейной регрессии являются уравнениями прямых линий в плоскости , проходящих внутри соответствующего корреляционного поля. Такие линии называются линиями регрессии.

Для того, чтобы полученные МНК оценки обладали желательными свойствами, сделаем следующие предпосылки об отклонениях :

1) величина является случайной переменной;

2) математическое ожидание равно нулю: ;

3) значения независимы между собой. Откуда вытекает, в частности, что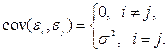

4) дисперсия постоянна: ;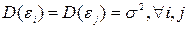

5) ошибки подчиняются нормальному распределению ~ 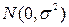(это условие не является обязательным, но оно необходимо для проверки статистической значимости найденных оценок и определения для них доверительных интервалов).

Если условия 1)-4) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами:

1. Оценки являются несмещёнными (т.е. математическое ожидание каждого параметра равно его истинному значению ).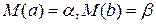

2. Оценки состоятельны (дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю: ). Иначе говоря, надёжность оценки при возрастании выборки растёт. Если n велико, то почти наверняка a близко к 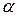, а b близко к .

3. Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра, линейными относительно величин .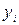

Пример 1.

По данным примера 1 оценить параметры уравнения линейной регрессии.

Тема 5. Оценка качества полученного уравнения (верификация)

Расчёт значений параметров уравнения регрессии – лишь первый шаг на пути решения проблемы количественного оценивания зависимости одной переменной от другой (других) переменных.

Следующим этапом решения этой проблемы является оценка качества построенного уравнения, вынесения суждения относительно его отдельных параметров и степени пригодности в целом.

Анализ качества оценённой зависимости включает статистическую и содержательную составляющие. Проверка статистического качества состоит из следующих элементов:

1. Проверка общего качества.

2. Проверка статистической значимости каждого коэффициента уравнения регрессии и всего уравнения в целом.

3. Проверка предпосылок, лежащих в основе МНК.

Под содержательной составляющей анализа качества понимается рассмотрение экономического смысла оценённого уравнения регрессии: действительно ли значимыми оказались объясняющие факторы, важные с точки зрения теории; положительны или отрицательны коэффициенты, показывающие направление действия этих факторов; попали ли оценки коэффициентов регрессии в предполагаемые из теоретических соображений интервалы.

Дата добавления: 2014-01-07