Оценка общего качества уравнения регрессии

Для анализа общего качества полученного уравнения регрессии на количественном уровне используют коэффициент детерминации 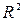. Он рассчитывается по формуле:

.

В числителе вычитаемой из единицы дроби стоит сумма квадратов отклонений (СКО) выборочных значений зависимой переменной от теоретических, найденных с помощью уравнения регрессии . В знаменателе – СКО наблюдений зависимой переменной от среднего значения.

Коэффициент детерминации характеризует долю вариации (разброса) зависимой переменной, объяснённой с помощью данного уравнения.

Замечание. В случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента линейной корреляции.

Более точным является значение коэффициента детерминации с поправкой на число степеней свободы.

Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы:

– дисперсия, характеризующая общий разброс;

– остаточная дисперсия, где m – число независимых (объясняющих) переменных, в случае парной регрессии m =1 и формула имеет вид: .

Учитывая приведённые выше обозначения, формула коэффициента детерминации с поправкой на число степеней свободы будет иметь вид:

.

Значения коэффициента 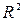изменяются от 0 до +1 (в редких случаях значение может быть и отрицательным числом).

Близость коэффициента детерминации к +1 свидетельствует о том, что существует статистически значимая линейная связь между переменными, а уравнение имеет хорошее качество.

Близость 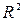к 0 говорит о том, что просто горизонтальная прямая 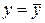является лучшей по сравнению с найденной регрессионной прямой.

Самостоятельную важность коэффициент детерминации приобретает только в случае множественной регрессии.

Дата добавления: 2014-01-07