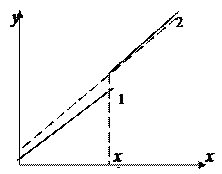Если качественная переменная имеет k альтернативных значений, то при моделировании используется только (k-1) фиктивных переменных

Например, если качественная переменная имеет 3 уровня, то для моделирования достаточно двух фиктивных переменных z₁ и z₂. Тогда для обозначения третьего уровня достаточно принять, например, обе переменные равными нулю: z₁ = z₂ =0. В частности, для обозначения уровня экономического развития страны (развитая, развивающаяся или страна «третьего мира») можно использовать обозначения:

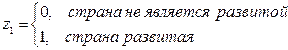
Тогда z₁=z₂= 0 означает страну «третьего мира».

Рассмотрим модель с двумя объясняющими переменными, одна из которых количественная, а другая – фиктивная, причем имеющая 3 альтернативы. Например, расходы на содержание ребёнка могут быть связаны с доходами домохозяйств и возрастом ребёнка: дошкольный, младший школьный и старший школьный.

Т.к. качественная переменная связана с 3 альтернативами, то по общему правилу моделирования необходимо использовать 2 фиктивные переменные:

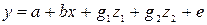, где у – расходы на содержание ребёнка, х – доходы домохозяйств,

, .

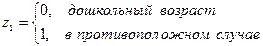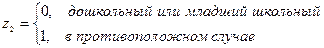Тогда образуются частные уравнения регрессии для отдельного возраста:

- расходы на дошкольника: ;

- расходы на младшего школьника: ;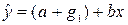

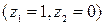- расходы на старшего школьника: .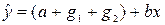

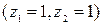Базовым значением качественной переменной является значение «дошкольник», - дифференциальные свободные члены. Т.о. получаем три параллельные регрессионные прямые:

a+g₁+g₂

После вычисления коэффициентов регрессий определяется статистическая значимость на основе обычных t – статистик. Если они оказываются статистически незначимыми, то можно сделать вывод, что возраст ребёнка не оказывает существенного влияния на расходы по его содержанию.

4. В отдельных случаях может оказаться необходимым введение двух и более фиктивных переменных.

Для простоты рассмотрим регрессию с одной количественной и двумя качественными переменными. Пусть у – заработная плата сотрудников, х – стаж работы, z₁ – наличие высшего образования, z₂ – пол сотрудника.

, .

Т.о. модель имеет вид: .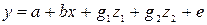

Из неё получаем следующие зависимости:

- зарплата женщины без высшего образования: ;

- зарплата женщины с высшим образованием: ;

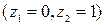- зарплата мужчины без высшего образования: ;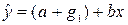

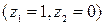- зарплата мужчины с высшим образованием: .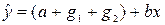

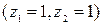Очевидно, что все отдельные регрессии отличаются друг от друга только свободным членом. Определение статистической значимости коэффициентов показывает, влияют ли образование и пол сотрудника на его зарплату.

5. Фиктивные переменные широко используются и для оценки сезонных различий в потреблении. Например, спрос на туристические путёвки, охлаждённую воду, мороженное существенно выше летом, чем зимой. Спрос на обогреватели, шубы – наоборот.

Обычно сезонные колебания характерны для временных рядов. Устранение и нейтрализация сезонного фактора позволяет сконцентрироваться на других важных количественных и качественных характеристиках модели (тренде).

Устранение сезонного фактора называется сезонной корректировкой. Существует несколько методов сезонной корректировки, одним из которых является метод фиктивных переменных.

Пусть у зависит от количественной переменной х, причём зависимость отличается по кварталам, тогда общую модель можно представить в виде:

,

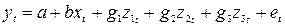где 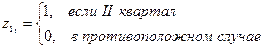, , 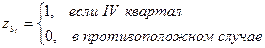. I квартал – база.

6. Иногда (достаточно редко) фиктивные переменные могут быть использованы для объяснения поведения зависимой переменной (т.е. зависимая переменная является фиктивной).

Например, исследуется зависимость наличия автомобиля от дохода, пола субъекта и т.п. Тогда .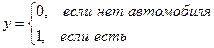

Такие модели являются вероятностными (линейными) моделями:

.

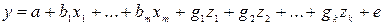Зависимая переменная у принимает значение 0 с вероятностью р и 1 с вероятностью (1– р).

Для оценки параметров линейно-вероятностной модели применяются методы Logit -, Probit-, Tobit- анализа.

7. Фиктивные переменные могут вводиться не только в линейные, но и в нелинейные модели, приводимые путём преобразования к линейному виду.

Например, .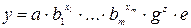

Логарифмируем, .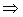

Наибольшими прогностическими возможностями обладают модели, зависящие от нескольких количественных факторов и от нескольких фиктивных.

Влияние качественного фактора может сказываться не только на значении свободного члена, но и на угловом коэффициенте линейной регрессионной модели. Обычно это характерно для временных рядов экономических данных при изменении институциональных условий, введении новых правовых или налоговых ограничений. Тогда зависимость может быть выражена так: ,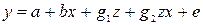

где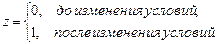

В этой ситуации ожидаемое значение зависимой переменной определяется следующим образом:

Коэффициенты g₁ и g₂ называются соответственно дифференциальным свободным членом и дифференциальным угловым коэффициентом. Фиктивная переменная разбивает зависимость на две части – до и после внесения изменений в условия её действия.

	х

Общая зависимость имеет вид кусочно – линейной функции, а изменения условий отображаются изменением угла наклона прямой к оси абсцисс (линии 1 – 2).

Здесь исследователь должен принять решение, стоит ли разбивать выборку на части и строить для каждой из них уравнение регрессии (прямые 1 и 2) или ограничиться одной общей линией регрессии (линия 3). Для этого используют тест Чоу, который опирается на F –статистику 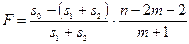, (см. тема «Статистика Фишера в регрессионном анализе»).

Если гипотеза о структурной стабильности выборки отклоняется, то исследуется вопрос о причинах структурных различий в подвыборках. Пусть данные в подвыборках описываются двумя уравнениями регрессии: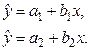

Тогда возможны следующие варианты:

1. Различие между а₁ и а₂ является статистически значимым, а коэффициенты b₁ и b₂ статистически не различаются. При этом наблюдается скачкообразное изменение зависимости при сохранении наклона линии регрессии.

2. Различие между b₁ и b₂ статистически значимо, а различие между а₁ и а₂ статистически незначимо.

3. Статистически значимыми являются и различия между а₁ и а₂, и различия между b₁ и b₂.

Для тестирования всех этих ситуаций применяется следующая методика, предложенная Гуйарати. Она основана на включении в модель регрессии фиктивной переменной z, которая равна 1 для всех x<x* и равна 0 для всех x>x ^*. Далее определяются параметры следующего уравнения регрессии: .

Отсюда видно, что а₁=(а+b); b₁=(c+d) (z=1),

a₂=a; b₂=b; (z=0).

Следовательно, параметр b есть разница между a₁ и а₂, параметр d – разница между b₁ и b₂. Если в уравнении b является статистически значимым, а d – нет, то имеем первый вариант структурной перестройки. Если, наоборот, статистически значимым является d, а b – незначим, имеем второй вариант структурных изменений. Наконец, третий вариант имеем в случае, если оба коэффициента b и d являются статистически значимыми.

В заключение следует отметить, что преимущество метода Гуйарати перед тестом Чоу состоит в том, что нужно построить только одно, а не три уравнения регрессии.

Дата добавления: 2014-01-07