Алгоритм устранения левой рекурсии

Домашнее задание: Написать алгоритм устранения правой рекурсии.

Вход: Приведенная КС-грамматика .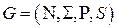

Выход: Грамматика 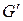без левой рекурсии (нелеворекурсивная грамматика).

Метод:

1. Пусть 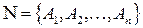(перенумеруем все нетерминалы).

Идея метода: Преобразуем грамматику 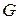так, чтобы в правиле цепочка 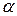начиналась либо с терминала, либо с нетерминала 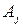такого, что и установим .

2. Рассмотрим множество правил для текущего нетерминала 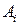. Если 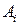является нелеворекурсивным, то никаких изменений во множестве правил 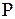не производим. Если 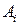является леворекурсивным символом, то множество правил для этого нетерминала можно представить следующим образом

.

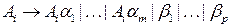Тогда вместо этих правил во множество 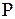добавляем правила вида

;

,

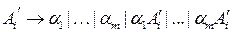где

- это новый нетерминал, который добавляется во множество нетерминалов ;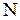

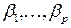- правые части правил для нетерминала 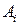, которые начинаются либо с терминала, либо с нетерминала, номер которого больше номера текущего нетерминала, т.е. с нетерминала 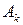, где ;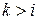

3. Если 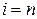, то алгоритм останавливается, и полученная грамматика 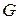будет результирующей ();

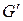если , то , вспомогательная переменная и переходим к шагу 4;

4. Для нетерминала 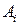находим все правила вида 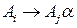, если 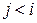, то делаем замену нетерминала 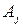в этих правилах, на правые части правил для нетерминала 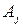, т.е. 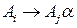заменяется правилами 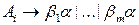, где все 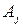-правила. Так как правая часть 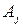-правила начинается с терминала, или с 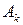, где 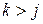, то и правая часть каждого 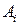-правила будет обладать этим свойством;

5. Если , то переходим к шагу 2,

если , то 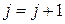и переходим к шагу 4.

Пример:

Выполнить устранение левой рекурсии в грамматике с правилами вывода вида

,

,

,

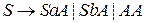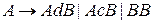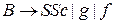где

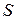- целевой символ.

Решение:

1. 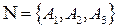, установим ;

2. Рассмотрим множество правил для нетерминала 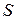, он является леворекурсивным символом, тогда множество правил для него запишется так

.

Добавляем во множество правила вида

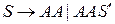
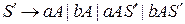
во множество ;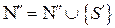

3. Так как , делаем приращение и задаем вспомогательную переменную ;

4. Для нетерминала 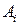находим правила вида 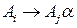и если 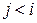, то сделаем замену, таких правил для текущего нетерминала нет;

5. Так как , то переходим к шагу 2;

2. Рассмотрим множество правил для нетерминала 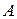, он является леворекурсивным символом, тогда множество правил для него запишется так

.

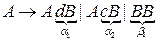Добавляем во множество правила вида

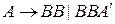
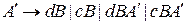
во множество ;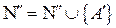

3. Так как , делаем приращение и задаем вспомогательную переменную ;

4. Для нетерминала 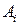находим правила вида 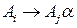и если 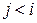, то сделаем замену, такие правила есть, тогда произведем замену правила вида

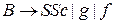
на правило вида

;

5. Так как , то осуществляем приращение вспомогательной переменной переходим к шагу 4;

4. Для нетерминала 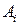находим правила вида 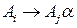и если 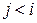, то сделаем замену, такие правила есть, тогда произведем замену правила вида

;

на правила вида

;

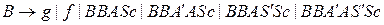5. Так как , то переходим к шагу 2;

2. Рассмотрим множество правил для нетерминала 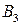, он является леворекурсивным символом, тогда множество правил для него запишется так

.

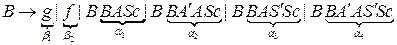Добавляем во множество правила вида

;

.

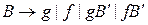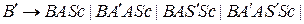
Множество ;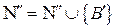

3. Так как 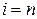, алгоритм останавливается, результирующая грамматика примет вид

,

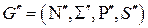где

;

;

;

.

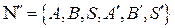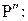
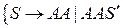
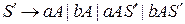
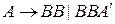
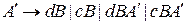
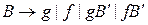
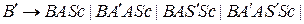
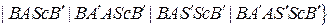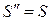Домашнее задание: Привести грамматику к нелеворекурсивному виду.

.

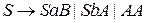
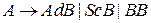
Домашнее задание: Привести грамматику к неправорекурсивному виду.

.

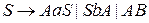
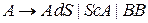
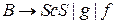Определение: КС-грамматика называется грамматикой в нормальной форме Грейбах, если множество правил данной грамматики удовлетворяет следующим условиям

1. ;, , ;

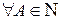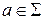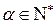2. ,

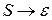где

1) ;

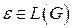2) 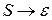- единственное правило такого вида;

3) 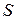- целевой символ данной грамматики;

4) 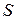- не встречается в правых частях других правил.

Дата добавления: 2014-01-07