
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм преобразования нелеворекурсивной приведенной КС-грамматики к нормальной форме Грейбах
|
|
|
|
Преобразование нелеворекурсивной приведенной КС-грамматики к нормальной форме Грейбах
Лемма: Пусть грамматика 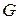 - нелеворекурсивная приведенная грамматика, тогда существует такой линейный порядок
- нелеворекурсивная приведенная грамматика, тогда существует такой линейный порядок  на
на 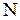 , что если имеется правило вида
, что если имеется правило вида
 ,
,
то
 .
.
Вход: Нелеворекурсивная грамматика 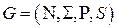 .
.
Выход: Грамматика  в нормальной форме Грейбах.
в нормальной форме Грейбах.
Метод:
1. Строим линейный порядок  на множестве нетерминалов
на множестве нетерминалов 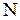 таким образом, что каждое правило для нетерминала
таким образом, что каждое правило для нетерминала 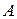 начинается либо с терминала, либо с нетерминала, для которого выполняется условие
начинается либо с терминала, либо с нетерминала, для которого выполняется условие
 .
.
Упорядочим  таким образом, что
таким образом, что
 ;
;
2. Полагаем  ;
;
3. Если 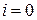 , то переходим к шагу 5;
, то переходим к шагу 5;
если  , то заменить каждое правило вида
, то заменить каждое правило вида 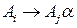 , где
, где  , правилами
, правилами 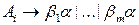 , где
, где - все правила для нетерминала
- все правила для нетерминала 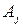 . Далее мы убедимся, что если каждая из цепочек
. Далее мы убедимся, что если каждая из цепочек  начинается терминалом, то и все правые части правил для нетерминала
начинается терминалом, то и все правые части правил для нетерминала 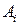 должны начинаться с терминала;
должны начинаться с терминала;
4. Положим  и переходим к шагу 3;
и переходим к шагу 3;
5. В результате выполнения шагов 3,4 все правые части каждого правила (кроме возможно 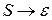 ) будут начинаться с терминалов. Для любого нетерминала
) будут начинаться с терминалов. Для любого нетерминала 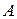 , если в правых частях правил терминал
, если в правых частях правил терминал  находится не на первом месте, то заменяем его на новый нетерминал
находится не на первом месте, то заменяем его на новый нетерминал  и в множество правил
и в множество правил 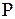 добавляется правило вида
добавляется правило вида

и записываем результирующую грамматику  .
.
Домашнее задание: Проверить результирующую грамматику, после удаления левой рекурсии.

 .
.
Пример:

 .
.
Решение: После выполнения алгоритма удаления левой рекурсии множество правил примет вид




1.  ,
,  ,
, 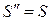 .
.
Строим линейный порядок  ;
;
2. Положим 
3. Так как  ,то вместо правил
,то вместо правил  добавляем в множество правил
добавляем в множество правил 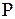 правила вида
правила вида
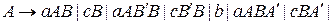
 ;
;
4. Положим  и переходим к шагу 3;
и переходим к шагу 3;
3. Так как  , то вместо правил
, то вместо правил  добавляем в множество правил
добавляем в множество правил 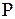 правила вида
правила вида




 ;
;
4. Положим  и переходим к шагу 3;
и переходим к шагу 3;
3. Так как  , то вместо правил
, то вместо правил  добавляем в множество правил
добавляем в множество правил 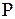 правила вида
правила вида
 ;
;
4. Положим  и переходим к шагу 3;
и переходим к шагу 3;
3. Так как 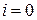 , то переходим к шагу 5;
, то переходим к шагу 5;
5. Выполняем замену всех терминалов 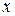 , которые находятся не на первом месте на новые нетерминалы
, которые находятся не на первом месте на новые нетерминалы  и в множество правил
и в множество правил 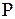 добавляются правила вида
добавляются правила вида
 .
.
Записываем результирующую грамматику 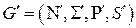 .
.
 ;
;
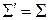 ;
;





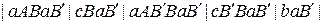





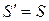 .
.
Недостаток: Недостаток описанной техники преобразования грамматики к нормальной форме Грейбах в том, что она дает много новых правил. Чтобы не вводить слишком много правил, можно применить другой метод, который излагается ниже. Однако он может давать больше нетерминалов.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2471; Нарушение авторских прав?; Мы поможем в написании вашей работы!