Производственная функция — это функция, описывающая зависимость количества продукта, которое может произвести фирма, от объемов затрат ресурсов

Технология и производственная функция. Изокванта и изокоста

Теория производства изучает прежде всего соотношение между кол ичеством применяемых ресурсов и объемом выпуска. Методически теория производства во многом совпадает с теорией

потребителя с тем, однако, отличием, что основные ее категории имеют не субъективно-психологическую основу, а объективную природу и могут быть квантифицированы, т. е. измерены, в определенных единицах.

Исходным пунктом такого анализа служит производственная функция. Она была разработана в 1890г. английским математиком А. Берри, помогавшим А. Маршаллу при подготовке математического приложения к работе "Принципы экономики".

Производственная функция во многом похожа на функцию полезности в теории потребителя. Это объясняется тем, что по отношению к ресурсам фирма ведет себя как потребитель и производственная функция характеризует именно эту сторону производства — производство как потребление.

Производственной функции присущи наиболее общие свойства функции полезности. Производственная функция описывает множество технически эффективных способов производства (технологий). Таким образом, технология отражает в натуральном выражении оптимальное (лучшее из всех возможны) сочетание факторов, используемое для производства выпуска некоторого заданного уровня. Следовательно, каждая технология характеризуется определенной комбинацией ресурсов необходимых для получения единицы продукции.

K

K₁

K₂

K₃

0 L₁ L₂ L₃ L

Рис. 6-1. Технология и производственная функция (изокванта)

В теории производства традиционно используется двухфакторная производственная функция, в которой объем производства — функция используемых ресурсов труда и капитала:

Графически каждый способ производства (технология) может быть представлен точкой, характеризующей минимальна необходимый набор двух факторов для производства выпуска данного объема (рис. 6-1).

На рисунке изображены различные способы производства (технологические лучи) Т_1, Т₂, Т₃, характеризующиеся равными соотношениями труда и капитала: Т₁ = L₁K₁; T₂ =L₂K_2; T₃=L₃K₃. Наклон технологического луча показывает интенсивность применения различных ресурсов. Чем выше клона луча, тем больше затраты капитала и меньше труда. Технология Т₁ более капиталоинтенсивна, чем технология Т₂.

Если соединить разные технологии линией, получится изображение производственной функции (линии равного выпуска), которая получила название изокванты. На рисунке которая объем производства Q₁ может быть достигнут при разной комбинации факторов производства (Т₁, Т₂, Т_ъ и т.д.). Верхняя часть изокванты включает капиталоинтенсивные, нижняя – трудноинтенсивные технологии.

Изокванты схожи по определению с кривыми безразличия, рассмотренными в теории потребителя. Так же, как кривые безраличия отражают альтернативные варианты потребительского выбора продуктов, обеспечивающие определенный уровень полезности, изокванты отражают альтернативные варианты затрат ресурсов для производства определенного объема продукции.

Карта изоквант — это совокупность изоквант, отражающая максимально достижимый выпуск продукции при любом дан­ном наборе факторов производства (рис. 7-2). Чем дальше изо-кванта от начала координат, тем больше объем выпуска. Изокванты могут проходить через любую точку пространства двух факторов производства. Смысл карты изоквант аналогичен смыслу карты кривых безразличия для потребителей, которая была рассмотрена в предыдущей главе.

Наклон изоквант характеризует предельную норму техниче­ского замещения, например, капитала К трудом L (MRTS_L,K):

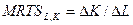
Данная формула означает, что увеличение затрат труда пол­ностью компенсирует уменьшение затрат капитала, так что в Результате объем выпуска остается на том же уровне.

Закон убывающей доходности. Прирост общего выпуска в связи с увеличением одного из факторов получил название предельного (дополнительного) продукта МР данного фактора. Доход, получаемый фирмой от использования дополнительного количества фактора производства, называется предельной производительностью (доходностью) фактора МКР. Предельная производительность вводимого фактора будет возрастать вплоть до некоторой точки. Но в конце концов по мере увеличения абсолютного значения переменного фактора достигается такая пределами которой дальнейший прирост переменного вводимого фактора производства ведет к сокращению доход от дополнительной единицы вводимого фактора. В экономической теории данное явление получило название закона убывающей доходности (производительности). Данный закон справедлив, по существу, для всех типов производственны функций: для сельскохозяйственного производства и автомобильной промышленности, розничной торговли и текстильных фабрик, предприятий по добыче природных ископаемых сферы услуг.

K

0 L

Рис. 6-2. Карта изоквант

Равновесие производителя обеспечивается тогда, когда он достигает максимума производства при имеющихся ресурсах.

Предположим, что производитель использует два фактора производства: 1 и 2. Каждый из факторов вносит определенный вклад в общий выпуск.

Предположим далее, что предельная производительность каждого из факторов составляет соответственно:

МКР₁ = 120 единиц продукции;

МКР₂ = 140 единиц продукции,

а их цены соответственно:

Р₁ = 10 долл.;

Р₂ = 20 долл.

Определим взвешенные (удельные) предельные производительности:

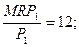
Из этого следует, что использование 1-го фактора более эффективно, чем 2-го. Предпринимателю целесообразно отказаться от одной единицы 2-го фактора, в результате чего он сэко­номит 20 долл. и сможет купить две единицы 1-го фактора, что повысит его прибыль. При этом потери составят 140 единиц продукции

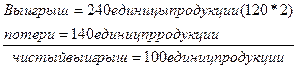
Таким образом, перераспределять ресурсы предприниматель будет до тех пор, пока взвешенные предельные производитель­ности не уравняются:

Правило наименьших издержек — это условие, согласно которому издержки минимизируются в том случае, когда последний рубль, затраченный на каждый ресурс, дает одинаковую отдачу — одинаковый предельный продукт.

Правило наименьших издержек обеспечивает равновесие производителя. Когда отдача всех факторов одинакова, их перераспределения не требуется, так как уже нет ресурсов, которые приносят большой доход по сравнению с другими.

Теперь сформулируем правило максимизации прибыли.

Сначала ответим на два вопроса:

а) в каком объеме нужен тот или иной ресурс для производства?

б) чем определяется степень его использования?

Фирма будет увеличивать использование ресурса до тех пока он будет приносить ей больший доход, чем затрать данный ресурс. Таким образом, степень использования ресурса фирмой определяется прежде всего разницей между доход который он приносит, и издержками, связанными с его использованием. Рациональный производитель стремится максимизи ровать эту разницу: наем дополнительного работника смысл, если доход, который он приносит, превышает издержки на его оплату.

В теории производства оптимум производителя определяется аналогично оптимуму потребителя в теории поведения и потребителя, т. е. равенством предельной нормы технически замещения одним ресурсом другого и соотношением их цен,

Пусть цена капитала К равна проценту r, а цена труда L-заработной плате W, тогда

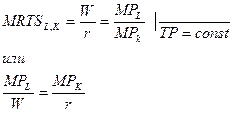
Это значит, что оптимум производителя достигается, когда последняя денежная единица, затраченная на труд, дает тот же прирост выпуска, что и последняя денежная единица, израсходованная на капитал.

Рассмотрим графическую иллюстрацию данного оптимума (рис. 7-3). Общие затраты на труд и капитал будут иметь вид:

Это уравнение бюджетного ограничения производителя. Из него выведем уравнение равных затрат (изокосты).

К

0 C/W L

Рис. 6-3. График изокосты

Фирма будет нанимать дополнительную единицу труда, если его предельная производительность MRP будет меньше издержек на заработную плату. Это значит, что цена ресурса (в данном случае заработная плата) измеряет его пре­дельную производительность. Если цену ресурса обозначим Р, то ресурс будет вовлекаться в производство до тех пор, пока

Отсюда следует условие максимизации дохода произво­дителя:

Смысл данного равенства заключается в том, что каждый ресурс используется до тех пор, пока его предельный продукт в денежном выражении не сравняется с иеной ресурса. Поэтому

опасно теории предельной производительности на каждый фактор производства приходится тот доход, который он создает.

Дата добавления: 2014-01-07