КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Особенности процесса нагревания при коротком замыкании
|
|
|
|
ТЕРМИЧЕСКАЯ СТОЙКОСТЬ ПРОВОДНИКОВ И АППАРАТОВ
Распространенные формы сечений проводников
При рабочих токах до 2000А широко применяются шины прямоугольного сечения с соотношением сторон 1/8, 1/10, 1/12, у которых kП < 1.1 и тепло эффективно отводится в окружающую среду, так как отношение поверхности к объему здесь больше, чем в шинах любой другой формы. Они легко соединяются между собой и присоединяются к аппаратам.
Составные проводники из двух полос имеют ограниченное применение. У них высок kП, сложнее монтаж. Из-за большого взаимного притяжения полос одной фазы приходится устанавливать большое количество дистанционных прокладок с соответствующим их креплением.
Пакеты из трех и четырех полос безусловно нецелесообразны вследствие значительного проявления поверхностного эффекта.
При рабочих токах, превышающих 2500 А, целесообразно применение трубчатых шин круглого и квадратного сечения. При очень больших токах (генераторы большой мощности) применяют только круглые экранированные алюминиевые трубы с толщиной стенки 15 мм и диаметром до 600 мм!
Ток замыкания в десятки раз превосходит рабочий ток. Тогда, в соответствии с (13), установившееся значение температуры будет в 100 и более раз выше рабочей, что означает разрушение проводника. Поэтому процесс нагрева прекращается в момент автоматического отключения поврежденного участка, после которого происходит относительно медленное остывание (рис. 2.6).

Рисунок 2.6 – Изменение температуры проводника при КЗ
Продолжительность КЗ обычно составляет доли секунды и, как исключение, может достигать нескольких секунд. Поскольку это время значительно меньше постоянных времени нагрева проводников (табл. 2.1) и аппаратов, то процесс нагрева происходит без теплоотдачи в окружающую среду по уравнению
 (15)
(15)
Поэтому необходим правильный выбор размеров токоведущих частей проводников и аппаратов для конкретных условий (величина тока КЗ, tОТК). Свойство проводников и аппаратов противостоять тепловому воздействию токов КЗ называется термической стойкостью.
На основании опыта установлены допустимые температуры нагрева:
неизолированные медные проводники - 300°С;
неизолированные алюминиевые проводники - 200°С;
кабели с бумажной пропитанной изоляцией до 10 кВ - 200°С;
провода и кабели с ПХВ изоляцией - 150°С,
то же, с полиэтиленовой изоляцией - 120°С.
Из (15) получим
 (16)
(16)
Учитывая, что
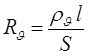 ,
,  ,
, 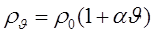 ,
,  , (17)
, (17)
где  - объем проводника;
- объем проводника; 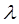 - удельный вес;
- удельный вес; 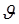 - температура;
- температура;  и
и  - удельные сопротивление и теплоемкость при 0°С;
- удельные сопротивление и теплоемкость при 0°С; 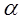 - температурный коэффициент сопротивления;
- температурный коэффициент сопротивления; 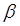 - температурный коэффициент теплоемкости.
- температурный коэффициент теплоемкости.
Подставив (17) в (16), получим
 или
или 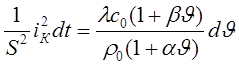 (18)
(18)
Интегрируем левую часть в пределах от 0 до  , а правую – от
, а правую – от  до
до 
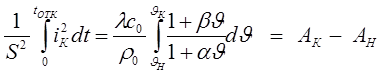 ,
,
где 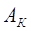 и
и 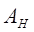 - конечный и начальный тепловые импульсы – значения правой части при
- конечный и начальный тепловые импульсы – значения правой части при 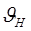 и
и  .
.
Здесь  – тепловой импульс тока КЗ или интеграл Джоуля, А2·с – численно равен количеству энергии, выделенной током в проводнике с сопротивлением 1 Ом в течение времени действия тока КЗ.
– тепловой импульс тока КЗ или интеграл Джоуля, А2·с – численно равен количеству энергии, выделенной током в проводнике с сопротивлением 1 Ом в течение времени действия тока КЗ.
|
(19)
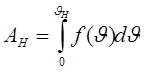 ,
,  , где
, где  (20)
(20)

Рисунок 2.7 – К пояснению значения выражений (20)
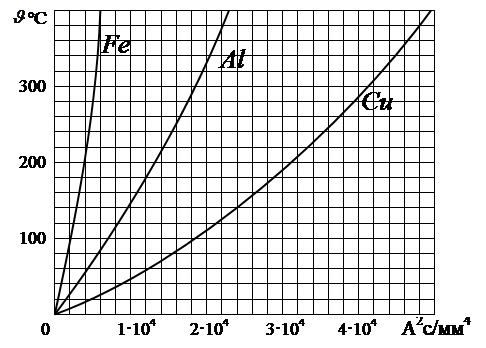 Используя рис.2.7, получим зависимости
Используя рис.2.7, получим зависимости 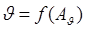 для различных проводников (рис. 2.8)
для различных проводников (рис. 2.8)
Рисунок 2.8 – Кривые для определения температуры нагрева проводников при КЗ
Расчет нагрева производим в следующем порядке:
1) зная 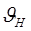 по кривым рис. 2.8 находим
по кривым рис. 2.8 находим 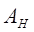 . Затем находим
. Затем находим 
2) по кривым находим  .
.
Если необходимо выбрать сечение из условия термической стойкости проводника для данного ВК
 ;
; 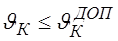 (21)
(21)
Если до КЗ протекал номинальный ток при номинальной температуре окружающей среды, то минимально-допустимое сечение проводника ST по условию термической стойкости можно найти из (21) как
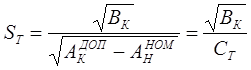 (22)
(22)
Таблица 2.3 -Допустимые температуры нагрева проводников при К. З. и значения СТ
| Проводники | 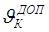 , 0 С , 0 С
| СТ, 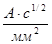
|
| Шины алюминиевые | ||
| Шины медные | ||
| Шины стальные | ||
| Кабели при UH ≤ 10кB(Al) | ||
| Кабели при UH ≥ 20кB(Al) | ||
| Провод из Al для ЛЭП |
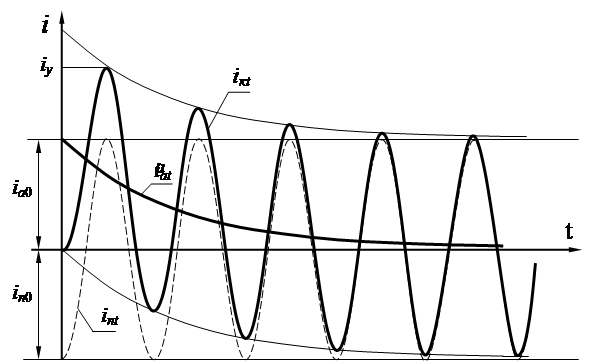 Тепловой импульс ВК (интеграл Джоуля) вычисляют по известному току КЗ.
Тепловой импульс ВК (интеграл Джоуля) вычисляют по известному току КЗ.
Рисунок 2.9 – Изменение тока КЗ в цепи, питаемой от неизменного напряжения при максимальном значении апериодической составляющей
В индуктивных цепях, к которым близки сети, максимальное значение периодической составляющей возникает, когда подключение происходит в момент перехода напряжения через 0 и когда тока в этот момент в цепи нет.
Ток КЗ состоит из двух составляющих:
периодической
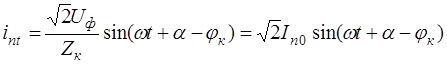 (23)
(23)
и апериодической
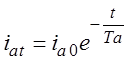 , (24)
, (24)
где 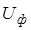 - фазное значение напряжения источника,
- фазное значение напряжения источника, 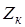 - сопротивление цепи,
- сопротивление цепи,  - фаза напряжения в момент времени 0,
- фаза напряжения в момент времени 0, 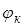 =90º - угол сдвига фаз между током и напряжением.
=90º - угол сдвига фаз между током и напряжением.
В нашем случае 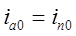 .
.
 (25)
(25)
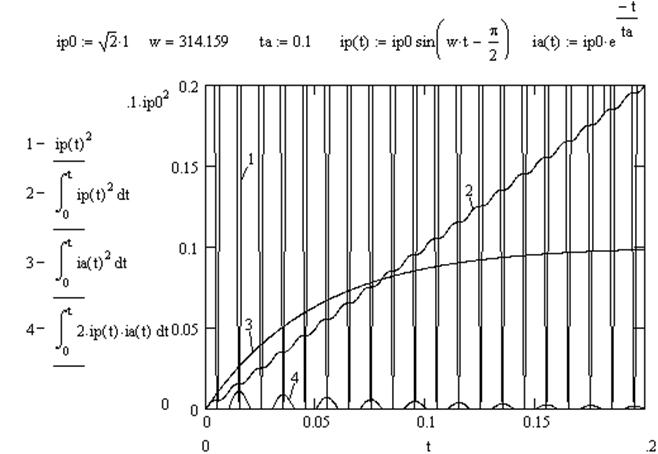
Из (25) следует, что тепловой импульс имеет три составляющих, поведение которых в течение десяти периодов приведено на рис.2.10.
Составляющая  в (25) имеет знакочередующийся характер, поэтому интеграл от нее, изображенный на рис. 2.10 (кривая 4) не увеличивается и имеет пренебрежимо малую величину. Вследствие этого считают, что тепловой импульс имеет периодическую и апериодическую составляющие
в (25) имеет знакочередующийся характер, поэтому интеграл от нее, изображенный на рис. 2.10 (кривая 4) не увеличивается и имеет пренебрежимо малую величину. Вследствие этого считают, что тепловой импульс имеет периодическую и апериодическую составляющие
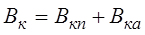 .
.
|
Рисунок 2.10 – Расчет составляющих теплового импульса при КЗ в пакете MathCAD
Для синусоидального тока тепловое воздействие от мгновенного значения равно тепловому воздействию от действительной составляющей при , поэтому импульс от периодической составляющей
, поэтому импульс от периодической составляющей

Условие  выполняется при расчете составляющей теплового импульса от системы. Однако для генераторов и синхронных компенсаторов периодическая составляющая будет затухать. В этом случае применяется графоаналитический метод [2, c.59]. Для ориентировочных расчетов можно принять
выполняется при расчете составляющей теплового импульса от системы. Однако для генераторов и синхронных компенсаторов периодическая составляющая будет затухать. В этом случае применяется графоаналитический метод [2, c.59]. Для ориентировочных расчетов можно принять
 .
.
При этом величина получится несколько завышенной, но уточнять ее, как правило, не требуется, поскольку проводники, выбранные в мощных присоединениях (генератор, трансформатор связи и т.д.) по условиям длительного режима и электродинамической стойкости имеют значительные запасы по термической стойкости.
С учетом того, что  , тепловой импульс от апериодической составляющей можно определить как
, тепловой импульс от апериодической составляющей можно определить как
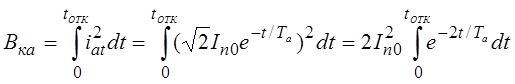
Для интегрирования заменяем переменные
 ,
, 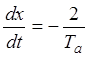 ,
, 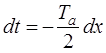 .
.
Тогда
 (26)
(26)
Как видно из выражения (26), тепловой импульс от апериодической составляющей затухает в два раза быстрее апериодического тока и после Ta уже не увеличивается. Обычно tОТК > Ta, поэтому с некоторым запасом принимают

и полный импульс квадратичного тока будет равен

 . (27)
. (27)
Известную трудность представляет определение постоянной времени Ta. Для ориентировочных расчетов можно принимать значения по таблицам [4, с.149-150], откуда следует, что для генераторов мощностью 100 – 300 МВт Ta = 0.26 – 0.36, а для системы на напряжениях 110, 220, 330 кВ Ta равно соответственно 0.02, 0.03 и 0.04 с.
Согласно ПУЭ время отключения (время действия токов КЗ) tОТК складывается из времени действия основной релейной защиты tР.З. данной цепи с учетом действия АПВ и полного времени отключения выключателя tОТК..В:
tОТК = tР.З. + tОТК..В.
В [4, с. 206-211] для различных зон действия защит приведены времена отключения. Так для шин генераторов tОТК = 4 с, для ОРУ – 0.1- 0.2 с, для нагрузки секций 6-10 кВ – 0.6-1.2 с.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2092; Нарушение авторских прав?; Мы поможем в написании вашей работы!