Принцип неразличимости одинаковых частиц. Принцип Паули. Распределение электроновв многоэлектронных атомах

В разделе квантовой механики, рассматривающем свойства систем, состоящих из большого числа частиц таких как: сложный атом, электрон­ный газ в металле, жидкий гелий, обнаруживший при низких температу­рах свойство сверхтекучести, прежде всего, следует учитывать принцип неразличимости одинаковых частиц.

Если частицы, описываемые классической механикой, тождест­венны между собой, то это вовсе не означает их неразличимости.

В квантовой механике понятие траектории отсутствует. Это при­водит к весьма глубоким изменениям при описании свойств системы многих микрочастиц.

Одинаковые микрочастицы принципиально неразличимы. Это ут­верждение и составляет содержание квантово-механического принципа неразличимости одинаковых частиц. Этот принцип проявляется в неизменности физических свойств системы при перестановке пары частиц. Волновая функция в этом случае может принять два значения:

Y(r₁, r₂) = Y(r_2, r₁) или Y(r₁, r₂) = -Y(r_2, r₁).

Функция системы, состоящей из двух частиц, приих перестановке или остается неизменной, или меняет знак на противоположный. Волновые функции, удовлетворяющие первому условию, называются симметричными, а удовлетворяющие второму условию – антисимметричными.

Частицы, свойства которых описываются симметричными функ­циями (к ним относятся мезоны, фотоны, атомные ядра, состоящие из четного числа нуклонов, и др.) называются частицами, подчиня­ющимися статистике Бозе – Эйнштейна, или бозонами. Антисимметрич­ными функциями описываются частицы, подчиняющиеся статистике Ферма – Дирака (к ним относятся электроны, позитроны, протоны, нейтроны, нейтрино и др.).

Для фермионов функция n, имеет вид: n = ,

а для бозонов n = .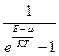

В этих выражениях m – химический потенциал системы, который пред­ставляет собой величину, численно равную изменению энергии в сис­теме при добавлении к ней одной частицы. Если число частиц пере­менно, то m = 0. Так, для фотонов, энергия которых равна E = ћw, получаем известное выражение Планка:

n = .

Заполнение энергетических уровней (оболочек) и элек­тронных орбиталей (подуровней) происходит согласно трем законам.

Первый закон – принцип Паули (1924 г., швейцарский физик).

В атоме не могут одновременно существовать электроны, характеризующиеся одинаковым значениемвсех четырех квантовых чисел.

Второй закон – правило Хунда. На одной электронной орбитали могут находиться два электрона с противоположными спинами. Общий спин атома, равный сумме спино­вых квантовых чисел всех его электронов, стремится быть максимальным.

Третий закон – принцип минимума энергии. Электроны в атоме стремятся занять положение с минимальным значением энергии, т.е. как можно ближе к ядру атома.

Принимая во внимание принцип Паули и учитывая 2 значения магнитного спинового квантового числа (m_{s = ±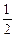}), принцип Пау­ли можно сформулировать и следующим образом: в атоме не может быть больше 2-х электронов, движение которых характеризуется одинако­вым значением 3-х квантовых чисел n, l, m_e.

Поскольку магнитное квантовое число m_e принимает 2 l +1 зна­чений, то в сложных многоэлектронных атомах число электронов, ха­рактеризующихся одинаковыми, значениями 2-х квантовых чисел n и l, не превышает 2 (2 l + 1).

Максимальное число электронов на энергетическом уровне, ха­рактеризуемое значением одного квантового числа n, может быть подсчитано из условия, что l = n - 1 или .

Эта сумма представляет сумму членов арифметической прогрессии, ко­торая может быть вычислена по формуле: S_n = 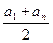n, тогда = 2 n = 2n², или представим таблицей:

Квантовые числа	Число электронов
n, l, me, ms
n, l, me
n, l	2(2 l + 1)
n	2n^2

Дата добавления: 2014-01-07