
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ функционирования автотранспортных систем доставки грузов
|
|
|
|
Методы анализа.
В научной и методической литературе используют различные методы анализа:
Ø однофакторного;
Ø многофакторного.
Однофакторный анализ заключается в исследовании влияния одного аргумента на величину функции.
Многофакторный анализ учитывает влияние нескольких факторов на величину функции.
При исследовании влияния технико-экономических показателей на выработку автомобилей, используется однофакторные методы анализа:
Ø метод цепных подстановок;
Ø метод относительных приращений;
Ø логарифмический метод;
Ø интегральный метод;
Ø и т.д.
Наибольшее распространение получил метод цепных подстановок.
Сущность метода заключается в следующем: анализируется влияние одного фактора (аргумента) на величину функции, при условном постоянстве величин остальных факторов, так последовательно анализируется влияние всех факторов (аргументов) функции.
Данный метод имеет определенные недостатки:
Например: не учет взаимосвязей различных факторов между собой.
Пример: При изменении грузоподъемности автомобиля изменяется время погрузки-выгрузки, а может и скорость. Однако в силу простоты метода, его допустимо использовать в теоретических исследованиях.
Анализ функционирования микросистемы.
Исследование расстояния перевозки грузов на выработку микросистемы. При установлении влияния различных факторов на функционирование системы используется математическая модель микросистемы.
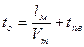 (110)
(110)
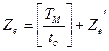 (111)
(111)
 (112)
(112)
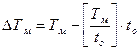 (113)
(113)
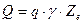 (114)
(114)
 (115)
(115)
В качестве исходных данных принимаем Тм=10, tпв=0,5, q=5т., γ=1, Vт=20км/ч. Рассмотрим как будут изменяться функции Q и P при изменении lге с учетом дискретного характера транспортного процесса.
| lге, км | Ze | Q, т | P, ткм |
По данным таблицы построим графические зависимости, описывающие изменения Q и P, как функций расстояния перевозки груза.

Как видно на графике обе функции описываются ломаными прямыми линиями и не носят непрерывного монотонного характера. На графике видно, что с ростом расстояния от 20 до 40км. Q уменьшилось в два раза, но это не компенсировалось увеличением P, величина которой в обоих случаях составляет 400ткм.. Пробег автомобиля также одинаков, следовательно одинаковы и эксплуатационные расходы, но доходы различны. Согласно построенным зависимостям наблюдается одновременное падение выработки Q и P. Пример: Расстояние 25 и 35км., а также с ростом расстояния Q может, не уменьшатся, а P может не возрастать.
Полученные результаты показывают одну из причин несоответствия расчетного плана с фактической работой подвижного состава.
Исследование влияния грузоподъемности подвижного состава и γ ее использования на эффективность работы микросистемы.
Q=f(qγ) (116)
P=f(qγ) (117)
Практическая деятельность при увеличении грузоподъемности и γ, изменяются также показатели скорость движения, время ПВ. При этом время ПВ, а скорость движения уменьшится. Это совокупное влияние может вызывать снижение выработки подвижного состава.
Изменение времени оборота в результате (qγ) можно проследить если воспользоваться следующим выражением:
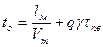 (118)
(118)
где: τпв – время простоя при ПВ 1т. Груза.
Влияние (qγ) на выработку транспортных средств в микросистеме рассмотрим на примере:
Тм= 9,2ч, τпв= 0,083ч, q= 5т, Vт= 23км/ч, lге1= 10км, lге2= 20км, lге3= 30км, γ=1.
Расчет производим по модели функционирования микросистемы.
| qγ, т. | lге1= 10км | lге2= 20км | lге3= 30км | ||||||
| Zе | Q | P | Zе | Q | P | Zе | Q | P | |
По данным таблицы построим графики зависимости Q и P от qγ.

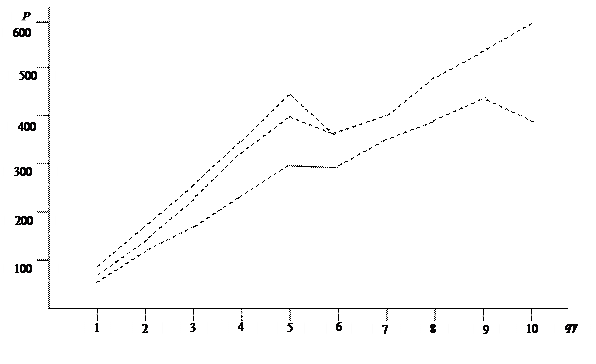
Выполненные расчеты и построенные графики позволяют сделать следующие выводы:
1. При выполнении перевозок в микросистеме, может не наблюдаться последовательного приращения выработки при росте qγ. Q и P могут не только возрастать, но и уменьшаться, а также оставаться без изменения.
2. Функции Q=f(qγ) и P=f(qγ) представляют собой прямые ломаные линии (кусочно-линейные зависимости).
3. С увеличением (qγ) возрастает время ПВ, что вызывает падение Zе за плановое время на маршруте. В результате, может оказаться, что автомобиль меньшей грузоподъемности в одних и тех же условиях эксплуатации может иметь большую выработку.
Выявленные закономерности объясняют почему от роста грузоподъемности транспортное средство и в частности применения автопоездов можно не получить ожидаемого эффекта.
Исследование влияния скорости на эффективность работы микросистемы.
Увеличение скорости движения автомобилей, как правило положительно влияет на их выработку, однако с ростом скорости увеличиваются затраты, поэтому необходимо выяснить всегда ли увеличение скорости вызывает такой прирост выработки за счет которого можно было бы окупить расходы связанные с ростом скорости движения подвижного состава.
Исходя из принципа, что за плановое время на маршруте автомобиль может выполнить только целое число ездок, можно утверждать, что приращение средне технической скорости, только тогда сопровождается ростом выработки, когда за счет сокращения затрат время движения, появляется возможность выполнить хотя бы одну ездку. В противном случае эффект только кажущийся и в действительности прироста выработки не будет, а только возрастут затраты на эксплуатацию.
Рассмотрим пример: измерение выработки автомобиля при следующих условиях. Тм= 10ч, γ=1, q= 5т, lге= 20км, tпв =0,5ч. При выполнении расчетов также использовалась модель функционирования микросистемы.
| Vт,км/ч | Zе,ед | Q,т | P,ткм |

Выводы по результатам расчетов и построенным графикам следующие:
1. Функции (Q и Р) f (Vт) являются разрывными линейными.
2. Имеются достаточно большие промежутки изменения Vт, которые не сопровождаются приращением выработки, не учет этого явления может приводить к ошибкам в анализе и планировании работы транспортных средств.
3. Если на маршруте автомобиль не может реализовать более высокую скорость, которой соответствует целое число ездок в данном примере 34км/ч., то он должен двигаться с меньшей скоростью, которой также соответствует целое число ездок.
Пример: 26км/ч. эта скорость будет экономически целесообразной, так как все промежуточные значения между 26 и 34км/ч. не дают роста выработки, а только сопровождаются необоснованными затратами. Это является основанием для понятия рациональная скорость.
Рациональная скорость Vp – это такая минимальная скорость, которой соответствует целое число ездок и выполнение перевозок с которой достаточно для исполнения доставки груза в системе за время ее работы.
Исследование влияния времени простоя при выполнении погрузочно-разгрузочных работ на эффективность функционирования микросистемы.
Функции (Q и Р) f (tпв).
При сокращении tпв имеется тенденция роста выработки подвижного состава.
Результаты проведенных исследований позволяют утверждать, что не всегда при сокращения затрат времени на погрузочно-разгрузочные работы, выработка возрастает. Эффект от уменьшения tпв получается только тогда когда за плановое время нахождения на маршруте в результате снижения tпв можно выполнить дополнительно хотя бы одну ездку. Если этого не происходит, то не вырабатывается дополнительной продукции, за счет которой можно было бы окупить средства затрачивыемые на организацию и механизацию погрузочно-разгрузочных работ.
tпв можно снизить следующими способами:
1. замена ручного труда на механический способ погрузки выгрузки;
2. замена погрузочно-разгрузочных механизмов на более современные и производительные;
3. рациональная планировка грузовых пунктов и рациональная расстановка автотранспортных средств в них.
Пример: Закономерность выработки транспортного средства: Тм =10ч., q =5т., γ =1, Vт =23км/ч., lге =15км.
Расчеты по модели микросистемы произведены в таблице:
| tпв, ч. | Ze,ед. | Q,т. | Р,ткм. |
| 0,3 0,4 0,5 0,6 0,7 0,8 0,9 |

Выводы: 1. Закономерность выработки автомобиля в т. и ткм. описываются разрывной линейной функцией.
2. На достаточно больших промежутках изменения tпв, выработка автомобиля не изменяется. Это означает что автомобили, работая на одном и том же маршруте при разном времени погрузки выгрузки, выработка не меняется.
3. В данном примере снижение простоя под погрузкой выгрузкой с 0,8 до 0,5ч. не дало эффекта в виде роста транспортной продукции, но привело к повышенным затратам, поэтому погрузочно-разгрузочные работы рационально выполнять при 0,8ч.
Анализ функционирования особо малой системы.
В особо малых системах, которые представляют собой кольцевые и все виды маятниковых маршрутов, кроме маятникового с обратным не груженым пробегом, на которых работает один автомобиль. Происходит аналогичное изменение выработки в т. и ткм. при росте или уменьшении (lге, qγ, Vт, tпв), то есть вид маршрута не оказывает существенного влияния на характер данных зависимостей.
Все закономерности соответствуют линейным или разрывным линейным функциям.
Всегда наблюдается промежутки приращения ТЭП, не вызывающие роста выработки, величина изменения Q находится в прямой зависимости от Ze выполняемых за время пребывания автомобиля на маршруте Q=qγ Ze.
Особенности работы автомобиля на маятниковых маршрутах различного вида и кольцевых маршрутах обусловили необходимость разработки модели работы автомобиля на данных маршрутах, то есть в особо малых системах.
Различаются в конфигурации маршрутов, приводят к тому, что за оборот выполняется разное количество ездок, однако эти различия могут быть учтены в обобщенной модели особо малой системы, применимой для всех маршрутов, где работает один автомобиль.
Модель функционирования особо малой системы:
 (119)
(119)
где: lм – длина маршрута;
∑lге – длина груженой i-ой ездки, n-количество груженых ездок за оборот;
∑lх – длина холостой j-ой ездки, m-количество холостых ездок за оборот;
 (120)
(120)
где: tо – время оборота;
lм – длинна маршрута;
VT – среднетехническая скорость;
∑tпв – время простоя под погрузкой выгрузкой при выполнении i-ой ездки за оборот;
n -число ездок за оборот.
 (121)
(121)
где: Тм – время работы на маршруте;
Тн – время работы в наряде;
Тнул – время на нулевые пробеги.
 (122)
(122)
где: lн1, lн2 – нулевые пробеги;
VT – среднетехническая скорость;
 (123)
(123)
где: Zо – количество оборотов;
Тм – время работы на маршруте;
tо – время оборота.
 (124)
(124)
где: Ze – количество ездок;
Zо – количество оборотов;
n – количество груженых ездок за оборот;
Ze´ - количество дополнительных ездок.
 (125)
(125)
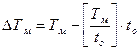 (126)
(126)
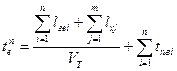 (127)
(127)
 (128)
(128)
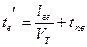 (129)
(129)
где: ΔТм – остаток времени после выполнения целого числа ездок;
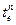 - время на дополнительную ездку;
- время на дополнительную ездку;
f – количество холостых ездок, которое должен пройти автомобиль чтобы выполнить k -ездок с грузом.
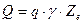 (130)
(130)
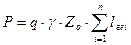 (131)
(131)
где: q – грузоподъемность;
γ – коэффициент грузоподъемности;
P – транспортная работа;
Q – грузооборот.
 (132)
(132)
где: Lобщ – общий пробег за сутки.
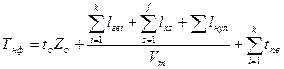 (133)
(133)
где: Тнф – фактическое время пребывания в наряде.
Анализ функционирования малой системы
Анализ влияния Vт на эффективность малой ненасыщенной системы.
В качестве примера рассмотрим работу автомобилей на маятниковом маршруте с обратным частично груженым пробегом: Тс =8ч., q =5т., γ =1, Vт =20км/ч., lге =15км, Аэ =4, tп=tв =0,5ч.
В малых системах в отличие от микро и особо малых систем необходимо учитывать возможность образования очереди в грузовых пунктах, чтобы избежать очереди в начале смены необходимо осуществлять выпуск автомобилей в определенной последовательности.
Кроме того, нужно иметь в виду, что время нахождения автомобиля на маршруте Тмi определяется моментом окончания работы разгрузочного пункта и для всех автомобилей возникает одновременно.
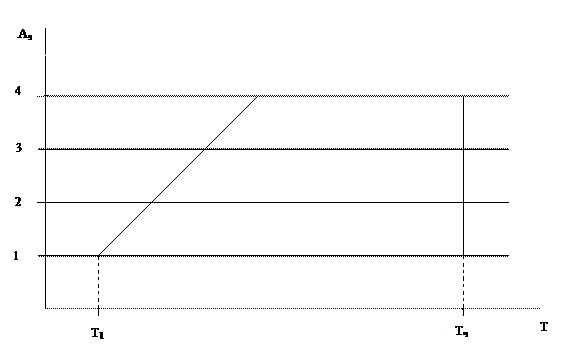
Максимальное время нахождения в системе первого автомобиля равняется времени системы, а последующих автомобилей.
Тм1=Тс (134)
Тмi=Tc-tn(i-1) (135)
Продолжительность нахождения автомобиля в системе составляет:
Тм1= 8
Тм2= 8-0,5=7,5
Тм3= 8-1=7
Тм4= 8-1,5=6,5
Используя модель, маятникового маршрута с обратным частично груженым пробегом, были произведены расчеты:
| Vт,км/ч | Zei,ед. | Ze,ед. | Q,т | |||

При возрастании Vт закономерность изменения выработки как для одного автомобиля, так и для системы в целом описывается разрывной линейной функцией, одновременно возрастает выработка автомобиля и системы, потребность в транспортных средствах не изменяется, но если объем перевозок ограничен, то может наблюдаться высвобождение автомобиля. Как видно на графике скорость движения автомобиля в системе может увеличиваться а, выработка нет (на интервале 22-24км/ч., 26-28км/ч.). При движении на скорости 30км/ч. система становится насыщенной, так как интервал движения при этом І=R.
График работы автомобиля при скорости 30км/ч.

На графике видно, что прибытие первого автомобиля под повторную погрузку происходит в момент окончания обслуживания четвертого автомобиля. Потому дальнейший рост скорости приведет к образованию очереди автомобилей в грузовых пунктах и потери времени, не говоря уже об экономических потерях связанных с повышенной скоростью движения.
В настоящее время в практике работы АТП принято всем выходящим на маршрут автомобилям выдавать одинаковое задание, но такое положение редко соответствует практической работе.
По таблице видно, что при скорости 22-24км/ч. выработка всех автомобилей в системе одинакова, а при других значениях скорости она различается.
Расчеты показывают, что не происходит одновременного повышения производительности всех автомобилей работающих в системе.
Выработка автомобилей зависит от того, каким по порядку автомобиль приступил к выполнению перевозок, а это указывает, что при работе группы автомобилей на каждый автомобиль должно рассчитываться индивидуальное задание. Коэффициент участия, с помощью которого оценивается деятельность каждого водителя при бригадном подряде, может быть одинаково, но за каждой долей коэффициента участия может быть разное количество работы.
Согласно таблицы на всем протяжении приращения скорости для третьего автомобиля не произошло ни какого изменения в выработки. Таким образом в малой системе эффект от увеличения скорости может быть не у всех автомобилей. Если, основываясь на этом положении увеличивать скорость только для тех автомобилей, у которых может произойти приращение выработки, то тогда окажется, что автомобили начнут прибывать в пункты погрузки выгрузки не последовательно, а стихийно, что приводит к образованиям очереди и потерям выработки.
Исследование функционирования малой насыщенной системы.
Исследование влияния скорости движения автомобиля на эффективность малой насыщенной системы. Количество постов равно 1.
Влияние скорости рассмотрим на примере маятникового маршрута с обратным не груженым пробегом: Тс =8ч., q =5т., γ =1, Vт =20км/ч., lге =10км., tпв =1ч., Аэ =4ед.

I=R

Построенный график указывает.
По окончанию в пункте погрузке четыре автомобиля совпадают со временем прибытия под повторную погрузку первого автомобиля. Как и в ненасыщенной системе, выпуск автомобилей, на линию осуществляя по графику последовательно через время погрузки.
В связи с этим продолжительность работы автомобилей в системе на маршруте будет разная.
Тм1=Тс
Тмi=Tc-tn(i-1)
Тм1= 8
Тм2= 8-0,5=7,5
Тм3= 8-1=7
Тм4= 8-1,5=6,5
По модели маятникового маршрута с обратным не груженным пробегом выполнены расчеты, результаты которых отражены в таблице.
| Vт,км/ч | Ze,ед. | ΣZe,ед. | |||
| … | … | … | … | … | … |
Результаты расчетов показывают, что в системе происходит рост числа ездок, как отдельных автомобилей, так и системы в целом. Однако в действительности таких явлений может не происходить.
Рассмотрим это на примере скорости 24км/ч.

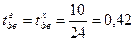
Первый автомобиль вернется в пункт погрузки, когда пост будет занят обслуживанием четвертого автомобиля, поэтому в пункте погрузки образуется очередь.
 (136)
(136)
mod – остаток от деления
to= 1,84
R= 0,5
mod =(to;R)= 0,34
tож= 0,16
В результате увеличения Vт все автомобили начинают терять часть времени в ожидании пунктов погрузки разгрузки, поэтому некоторым автомобилям может не хватать времени, чтобы выполнить количество ездок расчитаное без учета времени ожидания.
В данном примере третьему автомобилю не хватит времени, чтобы выполнить четыре ездки и фактически он сделает три. Поэтому повышение скорости не всегда приводит к положительному эффекту и выработка системы в целом остается неизменной.
В результате роста скорости может наступить момент, когда четвертый автомобиль будет не нужен. Он наступит, когда вновь будет соблюдаться соотношение І=R.

Для рассматриваемых условий высвобождение автомобиля произойдет при скорости 40км/ч. В связи с тем, что автомобилю нет необходимости выполнять холостой пробег на последней ездке, высвобождение автомобиля произойдет при скорости несколько меньшей, чем 40км/ч. Это будет 36км/ч.
С учетом потерь времени автомобилей в ожидании грузовых операций, произведем новый расчет Ze.
| Vт,км/ч | Ze,ед. | ΣZe,ед. | |||
| … | … | … | … | … | … |
С ростом скорости эффективность отдельных автомобилей возрастает, но это не приводит к росту выработки системы. При любой скорости количество ездок, выполненное автомобилями, равняется 14. увеличивать скорость до 34км/ч не рационально.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1368; Нарушение авторских прав?; Мы поможем в написании вашей работы!