Лекция 16. Практические рекомендации при использовании алгоритма ОРО

1. Выбор начальных значений. Этот этап оказывает влияние на достижение сетью глобального минимума функции ошибки и на скорость схождения к минимуму. С одной стороны, значения начальных весов не должны быть очень большими, иначе начальные входные сигналы в каждую скрытую или входную ячейку попадут в диапазон, где производная сигмоидной функции активации имеет очень малую величину. С другой стороны, если начальные значения взять достаточно малыми, то сетевой вход в скрытый или выходной нейрон будет ближе к нулю, что приведет к очень медленному обучению. Общее правило инициирования начальных весов заключается в выборе их значений из равномерно распределенных величин в интервале (-0,5…0,5) – иногда этот интервал может быть несколько меньше или больше, но не превышать 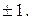Значения весов могут положительными или отрицательными, поскольку окончательные веса после обучения также могут иметь любой знак.

2. Продолжительность обучения сети. Предлагается использовать две серии данных во время обучения: серию обучающих образов и серию контрольных образов. Эти две серии являются раздельными. Регулирование веса основано на обучающих образах. Однако во время обучения ошибка вычисляется с использованием контрольных образов. До тех пор пока ошибка для контрольных образов уменьшается, процесс обучения продолжается. При возрастании этой ошибки сеть начинает терять свою способность к обобщению, и в этот момент обучение прекращается.

3. Количество требуемых обучаемых пар. Для соотношения между числом обучаемых образов Р, количеством регулируемых весов 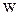и точностью классификации 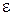предложено использовать следующее выражение: 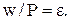Например, для 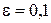многослойная сеть с 80 регулируемыми весами потребует 800 обучаемых образов, чтобы быть уверенным в правильной классификации 90% предъявляемых контрольных образов.

4. Представление данных. Для нейронной сети легче обучиться набору различных состояний, чем отклику с непрерывным значением.

Во многих задачах входные и выходные векторы имеют составляющие в одном и том же диапазоне величин. Вследствие того, что один из членов в выражении для корректировки весов является активацией ячейки предыдущего слоя, нейроны, имеющие нулевую активацию, обучаться не будут. Обучение может быть улучшено в том случае, если входной вектор представлен в биполярной форме, а в качестве функции активации используется биполярная сигмоида (биполярная сигмоида очень близка к функции гиперболического тангенса).

5. Введение инерционной поправки. Показано, что поиск минимума функции ошибок методом градиентного спуска оказывается достаточно медленным, если скорость обучения 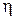мала, и приводить к значительным осцилляциям при большой скорости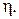

6. Модификация функции активации. Диапазон функции активации должен соответствовать диапазону целевых значений конкретной задачи. Бинарная сигмоидная функция вида 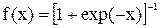с производной

Может быть изменена для перекрытия любого требуемого диапазона с центром при любом значении х и необходимом наклоне.

Сигмоида может иметь расширенный диапазон, чтобы отображать значения в интервале 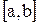для любых 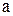и 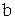. Для этого нужно ввести параметры

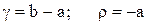
Тогда сигмоидная функция:

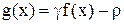
имеет требуемые свойства, т.е. диапазон 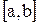. Ее производная выражается как:

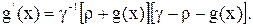
Наклон сигмоидной функции может быть изменен с помощью введенного параметра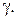

7. Число нейронов в скрытом слое. Подход при выборе скрытых нейронов заключается в том, что на первом этапе число таких нейронов берется заведомо большим, чем требуется, а далее, по мере обучения сети, излишние нейроны убираются. Все нейроны, которые не вносят вклад в решение или дают информацию, не требующуюся в последующем слое, рассматриваются как лишние и удаляются из скрытого слоя. На практике считается, что сеть достигла сходимости, если разность между требуемым и действительным выходами не превышает 0,1. Если два скрытых нейрона дают приблизительно одинаковый выход для всех обучающих примеров, то только один из них действительно необходим, так как оба нейрона переносят одинаковую информацию. После удаления тех ячеек, которые не дают вклада в решение, значения веса уменьшения сети должны быть изменены путем переобучения сети для получения требуемых характеристик.

Классический метод ОРО относится к алгоритмам с линейной сходимостью. Его известными недостатками являются: невысокая скорость сходимости (большое число итераций), возможность сходится не к глобальному, а к локальным решениям. Возможен также паралич сети – большинство нейронов функционируют при очень больших значениях аргумента функции активации, т.е. на пологом участке (т.к. ошибка пропорциональна производной, которая на данных участках мала, то процесс обучения практически замирает). Для устранения этих недостатков были предложены многочисленные модификации алгоритма ОРО.

Обучение без учителя. Главная черта, делающая обучение без учителя привлекательным, - это его «самостоятельность». Процесс обучения, как и в случае с учителем, заключается в подстройке весов синапсов. Очевидно, что подстройка весов синапсов может проводиться только на основании информации, доступной в нейроне, т.е. информации о его состоянии, уже имеющихся весовых коэффициентов и поданном векторе Х. Исходя их этого и по аналогии с известными принципами самоорганизации нервных клеток, построены алгоритмы обучения Хебба и Кохонена. Общая идея данных алгоритмов заключается в том, что в процессе самообучения путем соответствующей коррекции весовых коэффициентов усиливаются связи между возбужденными нейронами.

Дата добавления: 2014-01-07