Типы нейронных сетей

Многослойные нейронные сети – эти сети с сигмоидными передаточными функциями являются наиболее общими, универсальными сетевыми архитектурами. Имеются различные структуры многослойных сетей: с последовательными, перекрестными и обратными связями, с фиксированной и переменной структурой. С ростом числа слоев возрастают как сложность построения сети, так и качество ее работы. Многослойные нейронные сети являются универсальными аппроксиматорами.

Сеть Кохонена – кластерный анализ, распознавание образов, классификация. Слой Кохонена самообучается.

Нейронные сети встречного распространения – распознавание и восстановление образов, сжатие данных (с потерей информации), статистический анализ. Сеть содержит два слоя с последовательными связями: первый слой Кохонена, второй Гроссберга. Преимущества: 1) сеть проста; 2) сеть быстро обучается; сеть дает возможность строить функцию и обратную к ней функцию, что находит применение при решении практических задач. Недостатки. Слабая теоретическая проработка. Сеть не дает возможность строить точные аппроксимации.

Нейронные сети Хопфилда и Хемминга – позволяют просто и эффективно разрешить задачу воссоздания образов по неполной и искаженной информации.

Сети с радиальными базисными функциями (RBF) – двухслойная сеть без обратных связей, которая содержит скрытый слой радиально-симметричных скрытых нейронов (шаблонный слой). Сети RBF моделируют произвольную нелинейную функцию с помощью всего одного промежуточного слоя. Параметры линейной комбинации в выходном слое можно полностью оптимизировать с помощью хорошо известных методов линейной оптимизации, которые работают быстро и не испытывают трудностей с локальными минимумами, так мешающими при обучении с использованием алгортима ОРО. Поэтому сеть RBF обучается на порядок быстрее, чем с использованием алгоритма ОРО. Недостатками сетей RBF являются: сети обладают плохими экстрапалирующими свойствами и получаются весьма громоздкими при большой размерности вектора входов. Модификацией сети RBF является радиальная базисная сеть с нулевой ошибкой.

Другими модификациями являются вероятностные нейронные сети (PNN) и обобщенно-регрессионная нейронная сеть (GRNN).

Вероятностная нейронная сеть (PNN). Предназначены для решения вероятностных задач и, в частности, задач классификации. Архитектура сети PNN базируется на архитектуре базисной сети, но в качестве второго слоя используют так называемый конкурирующий слой, который подсчитывает вероятность принадлежности входного вектора к тому или иному классу, и, в конечном счете, сопоставляет вектор с тем классом, вероятность принадлежности к которому выше. Выходное значение имеет вероятностный смысл. Сеть быстро обучается. Недостатком таких сетей является их объем – сети требуют много памяти и могут медленно работать.

Обобщенно-регрессионная нейронная сеть (GRNN). Данная сеть аналогична вероятностной нейронной сети, но она предназнчена для решения задач регрессии. Как и сеть RBF, сеть GRNN не обладает способностью экстраполировать данные.

Линейные нейронные сети. Согласно общепринятому в науке принципу, если более сложная модель не дает лучших результатов, чем более простая, то из них следует предпочесть вторую. В терминах аппроксимации отображений самой простой моделью будет линейная, в которой аппроксимирующая (подгоночная) функция определяется гиперплоскостью. В задаче классификации гиперплоскость размещается таким образом, чтобы она разделяла собой два класса (линейная дискриминантная функция); в задаче регрессии гиперплоскость должна проходить через заданные точки. Линейная модель задается уравнением:

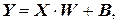
где 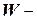матрица весов сети, 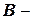вектор смещений.

На языке нейронных сетей линейная модель представляется сетью без промежуточных слоев, которая в выходном слое содержит только линейные элементы, т.е. элементы с линейной функцией активации. Веса соответствуют элементам матрицы, а пороги – компонентам вектора смещения.

Дата добавления: 2014-01-07