Функции моделирования НС

Примеры создания и использования нейронных сетей

Пакет Neural Networks Toolbox

Пакет Neural Networks Toolbox (нейронные сети) содержит средства для проектирования, моделирования, обучения и использования множества известных парадигм аппарата искусственных нейронных сетей, от базовых моделей персептрона до современных ассоциативных и самоорганизующихся сетей. Пакет может быть использован для решения множества разнообразных задач, таких как обработка сигналов, нелинейное управление, финансовое моделирование и т.п.

Для каждого типа архитектуры и обучающего алгоритма ИНС имеются функции инициализации, обучения, адаптации, создания и моделирования, демонстрации и примеры применения.

1. Функции создания нейронных сетей. Функции данной группы позволяют создать НС заданной структуры (необученную).

Синтаксис: Имя сети = функция (параметры сети)

Например, запись вида

net = newlind (p,t),

Описание: newlind – функция проектирования линейной НС. Данная функция по матрицам входных и выходных векторов методом наименьших квадратов определяет веса и смещения линейной НС.

net = newgrnn (p,t,spread) – функция создания обобщенно-регрессионной сети;

net = newrbe (p,t,spread) – функция создания сети с радиальными базисными элементами с нулевой ошибкой на обучающей выборке;

net = newpnn (p,t,spread) - функция создания вероятностной НС;

net = newp (pr,s,tf,lf) - функция создания персептрона (pr –матрица минимальных и максимальных значений входных элементов, s – число нейронов, tf – функция активации, по умолчанию пороговая, lf – функция, реализующая алгоритм обучения персептрона.

1. Sim - функция, моделирующая работу НС позволяет рассчитать выходы обученной НС при заданных векторах входов.

2. Gensim – функция формирует S-модель нейронной сети для ее запуска в среде Simulink.

Синтаксис: Gensim (net,st), где net – имя созданной сети, st – интервал дискретизации (если НС не имеет задержек, ассоциированных с ее входами или слоями, значение данного аргумента устанавливается равны -1). Функция генерирует нейросетевой блок Simulink для последующего моделирования НС средствами этого пакета.

Пример 1. Создать обобщенно-регрессионную НС (типа GRNN) с именем а, реализующую функциональную зависимость между входом и выходом вида 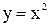. Синтаксис: net = newgrnn(p,t,spread), где p – матрица входных векторов, t – матрица целевых векторов, spread – отклонение (по умолчанию 1,0). Использовать следующие экспериментальные данные:

x=[-1 -0.8 -0.5 -0.2 0 0.1 0.3 0.6 0.9 1];

y=[1 0.64 0.25 0.04 0 0.01 0.09 0.36 0.81 1].

Проверку качества восстановления приведенной зависимости осуществить, используя данные контрольной выборки x1=[-0.9 -0.7 -0.3 0.4 0.8].

Процедура создания и использования данной НС описывается следующим образом:

>> x=[-1 -0.8 -0.5 -0.2 0 0.1 0.3 0.6 0.9 1]; задание входных значений

>> y=[1 0.64 0.25 0.04 0 0.01 0.09 0.36 0.81 1]; задание целевых значений

>> a=newgrnn(x,y,0.01); создание НС с отклонением 0,01

>> y1=sim(a,[-0.9 -0.7 -0.3 0.4 0.8]) опрос сети

y1 =

0.8200 0.5049 0.0316 0.0710 0.6390

Как видно, точность аппроксимации в данном случае получилась не очень высокой. Попробуем использовать сеть с радиальными базисными элементами типа newrbe:

>> a=newrbe(x,y);

>> y1=sim(a,[-0.9 -0.7 -0.3 0.4 0.8])

y1 =

0.8100 0.4900 0.0900 0.1600 0.6400

Нетрудно видеть, что применение сети данного типа приводит к точному восстановлению заданной зависимости.

Пример.2. Рассмотрим задачу восстановления некоторой, вообще говоря, неизвестной зависимости по имеющимся экспериментальным данным с использованием линейной НС. Пусть экспериментальная информация задана значениями

x = [1.0 1.5 3.0 -1.2],

y = [0.5 1.1 3.0 -1.0]

Создадим векторы входа и целей:

>> x=[1.0 1.5 3.0 -1.2];

>> y=[0.5 1.1 3.0 -1.0];

Создадим линейную нейронную сеть:

>> b=newlind(x,y); Создание НС с именем b.

Проведем опрос сети для значения входа, равного 3,0 (этому, согласно экспериментальным данным, соответствует целевое значение 3,0):

>> y1=sim(b, 3.0) Опрос сети

y1 =

2.7003

Погрешность восстановления по данным обучающей выборки в данном случае - 10%.

Дата добавления: 2014-01-07