Соединения ( комбинаторика )

Выражающая связь между случайными событиями и их вероятностями.

Наука, выражающая связь между случайными и достоверными событиями;

Частота события; 2) относительная частота события; 3) вероятность события; 4) относительная вероятность события.

Тесты

7. Как в теории вероятностей называется отношение числа m появлений некоторого события в серии опытов к общему числу опытов n?

8. Выберите правильное определение теории вероятностей:

2) наука, изучающая закономерности скрытой предопределённости;

3) наука, изучающая свойства случайных событий, могущих повторяться многократно при воспроизведении определённых условий;

9. Вероятность выпадения “3” при бросании игральной кости равна:

1) 1/3; 2) 1; 3) 1/2; 4) 1/6.

10. В ящике находятся 12 стандартных и 4 бракованных деталей. Из ящика наугад вынимают одну деталь. Какова вероятность того, что эта деталь стандартная?

1) 1/4; 2) 1/3; 3) 3/4; 4) 2/3.

11. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее четырёх очков равна:

1) 1/6; 2) 1/3; 3) 1/2; 4) 2/3.

12. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет более двух очков равна:

1) 1/6; 2) 1/3; 3) 1/2; 4) 2/3.

13. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более двух очков равна:

1) 1/6; 2) 1/3; 3) 1/2; 4) 2/3.

При непосредственном подсчёте числа комбинаций часто бывает полезно воспользоваться теорией соединений.

1. Перестановки. Перестановками из n элементов называются такие соединения, каждое из которых содержит все n элементов, и которые отличаются друг от друга лишь порядком элементов. Число перестановок находится по формуле 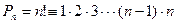. Считается, что 0! = 1.

П р и м е р. Из цифр 1, 3, 5, 7 при условии, что каждая цифра используется только один раз, можно составить 4! = 24 четырёхзначных чисел.

2. Размещения. Размещениями из n элементов по k элементов называются такие соединения, каждое из которых содержит k элементов, взятых из данных n элементов, и которые отличаются друг от друга либо самими элементами, либо порядком их расположения. Число размещений находят по формуле 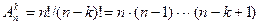, где k £ n.

П р и м е р. Из цифр 1, 3, 5, 7, 9 при условии использования каждой из цифр только один раз можно составить 5! / (5-3)! = 5 × 4 × 3 = 60 трёхзначных чисел.

3, Сочетания. Сочетаниями из n элементов по k элементов называются такие соединения, каждое из которых содержит k элементов, взятых из данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом. Их число определяют по формуле 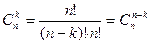. 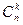называют биномиальным коэффициентом. 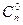==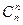1.

П р и м е р. Число вариантов зачёркивания 3 чисел в таблице из 9 разных чисел совпадает с числом вариантов зачёркивания 6 чисел и равно 9! / (3!×6!) = 84.

Дата добавления: 2014-01-07