Кіріспе 2 страница

Мұнда, бір масштабта көлденең осі бойымен гармоника жиіліктерімен шектелген. Ал тік осі бойымен олардың амплитудалары және бастапқы фазалары. Периодты сигналдардың спектрлік жіктелуін жалған көрсеткіштері бар экспонентен құралған Базисті функциялардың жүйесін қолданып оындауға болады:

(3.13)

Бұл жүйенің функциялары T периоды мен периодты және [-Т/2, Т/2] уақыт кесіндісінде ортонормаланған. Өйткені:

.

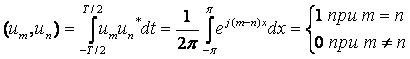Берілген жағдайда кездейсоқ периодты сигналдың Фурье қатарының түрі:

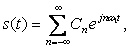(3.14)

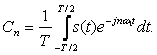(3.15)

(3.14) теңдігі жиынтық пішініндегі Фурье қатары деп аталады.

4 Дәріс. Периодты емес сигналдардың спектрлік анализі. Фурье түрлендіргіші интегралданбайтын сигналдардың спектрлі жазықтығы. Сигналдардың энергетикалық спектрі

Дәрістің мазмұны:

- импульстің периодты созылуының жалғасуы. Жазық спектрі сигнал туралы түсінік. Кері Фурье түрлендіруі. Сигналдың спектрлі жазықтығының бар болу шарты. Импульс ұзақтығы мен спектр енінің арасындағы байланыс. Рэленің жалпы формуласы. Сигналдардың өзара спектрлі жазықтығы. Энергетикалық спектр. Сигналдардың корреляциялық анализі. Уақыт бойынша ығысатын сигналдарды салыстыру.

Дәрістің мақсаты:

- Фурье қатарына жалпылау әдісі арқылы периодты емес (импульсті) сигналдардың спектрлік сипаттамасын алу. Радиотехникалық құрылғыдағы өткізу жолағы еніне қойылатын талапты анықтау. Сигналдарды спектрлі жазықтық әдісі бойынша түсіндіру. Әр түрлі инженерлік баға беру үшін энергетикалық спектрді қолдану. Арнайы таңдалған сипат бойынша сигналдарда қажеттілік қалай пайда болатынын түсіну.

S(t)-шекті ұзақтылықты жалғыз импульсті сигнал. Ойша оны кейбір Т интервал уақытындағы сигналдармен толықтырып, алдында қарастырылған периодты жүйе S(t) -ны аламыз. Ол кешенді түрдегі Фурье қатары ретінде берілуі мүмкін:

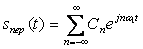, (4.1)

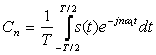. (4.2)

Жалғыз импульсті сигналға қайта оралу үшін Т қайталану периодың ұмтылдырамыз. Бұл жағдайда:

а) nω₁ және (n + l)ω₁ көрші гармоникаларының жиіліктері жақын болғандықтан (4.1) және (4.2)формулаларындағы nω₁-дискретті айнымалыны ω-кезекті жиіліктің үздіксіз айнымалысы ауыструға болады.

б) 4.2 формуласының бөліміндегі Т шамасының C_n амплитудалық коэффициенті шексіз кіші болады. Біздің мақсатымыз (4.1) формуласының шектік түрін табу T→∞. ∆ω жиіліктің кейбір таңдалған мәнінен туындаған ω₀ аймағындағы жиілігінің кіші аралығын қарастырамыз:

.

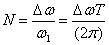Бұл аралықтың шегінде жиіліктері аз ерекшеленетін спектрлі құраушылардың жеке жұптары сипатталады. Сондықтан құраушылардың барлығы бірдей жиілікке ие және бірдей комплексті (кешенді) амплитудамен сипатталады деп қарастыруға болады:

.

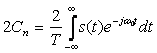Қорытындысында аралығы ішінде болатын барлық спектрлі құраушыларды бейнелейтін баламалы гармоникалық сигналдың кешенді амплитудасын табамыз:

. (4.3)

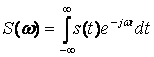. (4.4)

S(t) cигналдың спектрлі жазықтығы деген атқа ие (4.4) формуласы берілген сигналда Фурье түрлендіруін іске асырады. Спектрлі сигнал теориясының кері есебін шешеміз:

.

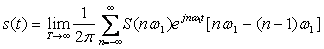Түрінде берілген есептеу спектрлі жазықтығы бойынша сигналды табамыз. Көршілес гармоникалар арасындағы шекте жиіліктік аралық шексіз деп қарастырылғандықтан, соңғы қосындыны

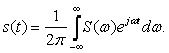(4.5)

ауыстыруға болады. Бұл маңызды формула сигналы үшін Фурье түрлендіру деп аталынады. Ақырғы іргелі қорытындыны шығара келе сигнал және оның спектрлі жазықтығы Фурьенің кері және түрлендіруімен өзара байланысты:

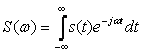, (4.6)

.

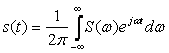Сигналдарды спектрлі деп елестету оларды радиотехникалық тізбек, құрылғы және жүйе арқылы өтеді деп қорытындылауға жол ашады. Егер сигналы абсолютті интегралданатын болса, оны спектрлі жазықтығына қоюға болады. Бұл жағдайда: |s(t)|dt<∞ интегралы бар болады. Бұл шарт өткізу сигналдар үшін қызмет етеді. Көрсетілген классикалық мағынада барлық шексіз ось уақытында бар болатын u(t)=U_mcosω₀t гармоникалық сигналдың спектрлі жазықтығы туралы айтпау мүмкін емес. Маңызды қорытынды: Импульстің ұзақтығы аз болған сайын спектрдің ені көбірек өзгереді. Спектрдің ені арқылы жиілікті аралықты білуге болады. Ол үшін спектрлі жазық модулі алдынғы берілген кейбір деңгейдің шегінен аз болмау керек. Мысалға (S)_max – 0,1(S)_max дейінгі аралықты өзгереді.

ƒ_вτ_u=0(1) бірлік реттігі бар тек импульс түріне қатысты болатын спектр импульсі енінің оның ұзақтығына туындысы тұрақты сан мәнімен сипатталады. Импульстің ұзақтығы қысқарған сайын сәйкесінше күшейткіштің өткізу жолағы ендірек болуы тиіс. Қысқа импульсті бөгеуілдер кең спектрға ие, сондықтан қажетті жиілік жолағында радиоқабылдау шарты нашарлауы мүмкін. Радиотехникада кең қолданылатын көптеген сигналдардың математикалық модельдері абсолютті интегралдау шартын қанағаттандырмайды. Сондықтан қарапайым түрдегі Фурье түрлендіруін оларға қолдануға келмейді. Егер бұл жазықтықтар жалпылама функциямен сипатталса, сигналдардың спектрлі жазықтығы туралы айтуға болады. Өздерінің кері Фурье түрлендіруімен анықталған u(t) және v(t) екі сигналы жалпы жағдайда кешенді мәнді болсын. Екеуінің біреуін, мысалға v(t)-ны спектрлі жазықтықпен сипаттап, скаляр туындысын табамыз.

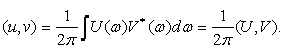
Бұл табылған қатынас Рэленің жалпы формуласы болып табылады. Бұл формуланы есте сақтаудың жолы мынадай: екі сигналдың скаляр туындысы коэффициентіне дейінгі дәлдікпен, олардың спектрлі жазықтығының скаляр туындысына пропорционал. Егер сигналдар сәйкес келсе, онда скаляр туынды энергияға тең болады:

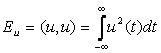. (4.7)

U(t) және v(t) функцияларын нақты сигналдардың өзара энергетикалық спектрі деп атайды.

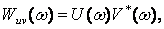(4.8)

Сондай,

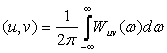. (4.9)

Re W_uv(ω)- жұп, ал Im W_uv(ω)- тақ жиілік функциясы екенін аңғару оңай. (4.9) интегралына қою тек нақты бөлігін береді. Сондықтан

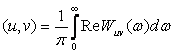. (4.10)

Соңғы формула сигналдардың өзара байланыстылығынын құрылымын алын ала қорытындылауға мүмкіндік береді. (4.10) түрінде берілген Рэленің жалпы формуласы олардың ортогональдығынын шегіне жеткен екі сигнал аралығындағы байланыс дәрежесіне төмендету жолын көрсетеді. Ол үшін сигналдың біреуін жиіліктік сүзгі деп аталатын ерекше физикалық жүйеде өңдеу керек. Сүзгіге қойылатын талаптар: жиіліктік аралықтың шегінде орналасқан спектрлік құраушыны шығысқа жіберу керек. Мұндай жиіліктік тәуелділікті ортогонализденетін сүзгінің беріліс коэффициенті көрсетілген жиілік аймағында минимуммен сипатталады.

U(t) және v(t) сигналдарын бірдей деп есептеп Рэленің жалпылама формуласының энергияның спектрлі көрсетілуін алуға болады. Энергияның спектрлі жазықтығын білдіретін формула мынандай түрге келеді:

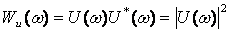. (4.11)

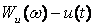сигналының спектрлі жазықтық энергиясы немесе оның энергетикалық спектрі. Осыдан (3.2) формуласы былай жазылады:

. (4.12)

(4.12) қатынасы Рэле формуласы (тар мағынада) және мынаны білдіреді: Сигналды энергетикалық спектр көмегімен оқығанда, оның фазалық спектріндегі ақпаратты жоғалтамыз.

(4.11) формуласынан энергетикалық спектр дегеніміз – спектрлі жазықтықтың квадрат модулі және оның фазасына қатысты емес. Қашықтықтан белгілі бір нысанаға дейінгі өлшеуге арналған импульсті радиолокатордың қысқартылған жұмыс әдісіне жүгінейік. Мұнда өлшеу нысаны туралы ақпарат τ-шамасына қатысты. τ -зондтайтын және қабылданған u(t–τ) сигнал арасындағы уақыт бойынша кідіріс. Зондтаушы u(t) және қабылданған сигналдарды түрі кез келген кідірісте бірдей.

Қашықтықты өлшеуге арналған радиолокациялық сигналдарды өңдейтін құрылғының құрылымдық сұлбасы (4.1суретті қара) көрсетілген.

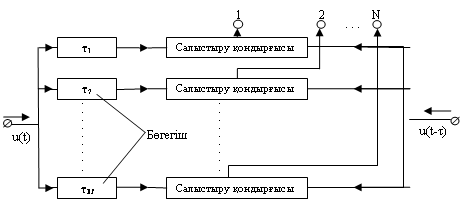
4.1Сурет - Сигналдың кешігу уақытын өлшейтін құрылғы

5 Дәріс. Корреляциялық талдаудың принципі. Кездейсоқ процестер және олардың негізгі сиппаттамалары

Дәрістің мақсаты:

- сигналдың автокорреляциялық функциясы. Сигналдың энергетикалық спектрі және оның корреляциялық функциясы арасындағы байланыс. Екі сигналдың өзара корреляцияланған функциясы. Кейбір өзара корреляцияланған функциялардың сиппаттары (қасиеттері). Өзара корреляцияланған функциялардың өзара спектрлі тығыздығымен байланысы. Кездейсоқ процесс түсінігі. Ықтималдықтың тығызығы және таралудың интегралдық функциясы.

Дәрістің мақсаты:

-автокорреляциялық функциямен сигналдың энергетикалық спектрі арасында өте тығыз байланысы бар екенін көрсету. Екі сигналдың жиынтығының ерекше сипаттамасын-олардың өзара корреляцияланған функциясын енгізу. Сигналдың детерминирленген сипаттамасы мүмкін емес болғанда және оның орны ықтималды сипаттамасымен ауыстырылатын жағдайдағы хабарды таратудағы көріністі оқып білу. Статикалық радиотехника есептерінде қолданылатын ықтималдылықтар теориясының негізгі түсініктерін оқып білу. Кездейсоқ көп өлшемді шамалардың жиынтығын оқи отырып, кездейсоқ сигналдың қасиетін сипаттау.

Сигналдың U(t) мөлшерлі айырмашылық деңгейін анықтау үшін U оның көшірме уақытындағы U(t–τ) ығысқанда автокорреляцияллық функция енгізу керек. Ол сигналдың скалярлық туындысы мен көшірмесіне тең:

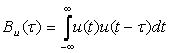. (5.1)

Ары қарай зерттелетін сигнал уақыт бойынша жергілікті импульстік сипатқа ие деп есептейміз. Сондықтанда түріндегі интеграл бар. АКФ-ң қарапайым сипаттамаларының қатарына оның жұптылығын жатқызуға болады:

B_u(τ)=B_u(-τ). (5.2)

Енді автокорреляциялық функцияның маңызды қасиеті келесіден тұрады:

Кез-келген уақыттық ығысу мәнінде АКФ модулі сигнал энергиясынан артық болмайды. Бұл кезде сигнал U(t) түріне байланысты автокорреляциялық функция монотонды кемімелі. Сонымен қатар тербелмелі сипатқа да ие бола алады.Шындығында (5.1) теңдігіне сәйкес АКФ бұл скалярлық туынды:

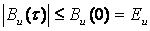. (5.3)

Бұл жерде U_τ белгісі ретінде уақыт бойынша ығысқан сигналдың көшірмесі U(t–τ) белгіленген.

Рэле формуласынан мына теңдікті алуға болады:

.

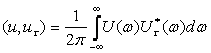Сигналдың уақыт бойынша ығысқан спектральді тығыздығы 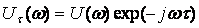бұл жерде .

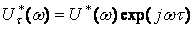Осыған байланысты мынадай шешімге келеміз:

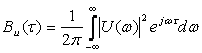. (5.4)

Бізге белгілі спектральды тығыздық модулінің квадраты сигналдың энергетикалық спектрін береді: Сонымен, энергетикалық спектр және автокорреляциялық функция Фурье түрлендірілуімен байланысты:

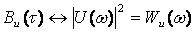. (5.5)

Кері ара-қатынаста болады:

. (5.6)

Бұл шешім екі себепке байланысты принципиальды маңызды.

Біріншіден: спектр бойынша олардың энергияларының таралуын есепке алмай сигналдың корреляциялық қасиетін бағалауға мүмкіндік бар. Сигналдың жиіліктер жолағы кең болған сайын, автокорреляциялық функция.

Екіншіден (5.4) және (5.6) формулалары энергетикалық спектрді эксперементальді анықтауға жол көрсетеді. Көбінесе басында автокорреляциялық функцияны алу, ал содан кейін Фурье түрлендірілуін қолданып, сигналдың энергетикалық спектрін табу ыңғайлы.

(5.1) формуласын жалпылай отырып оны екі сигналдың U(t) және V(t) скалярлық туындысын өзара корреляциялық функциясы (ӨКФ) деп атап, келесі түрде аламыз:

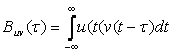. (5.7)

Егер (5.7) формуласындағ интегралдаушы айнымалыны х = t-τ деп ауыстырып, dt=dx деп алатын болсақ, онда келесі өрнекті аламыз.

. (5.8)

Сондықтан:

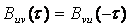. (5.9)

Жалғыз сигналдың автокорреляциялық функциясының ӨКФ-дан айырмашылығы екі бірдей емес сигналдар жүйесінің сипатталатын қасиеті 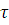аргументінің жұп функциясы болып табылмайды:

.

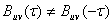Егер қарастырылатын сигналдардың ақырғы энергиялары болса, онда өзара корреляциялық функция шектелген. Бұл мақұлдылық Коши-Бунянковский теңсіздігінен шығады:

.

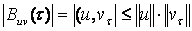Бұл жерде,

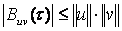. (5.10)

Себебі уақыт бойынша сигнал ығысуы оның нормасының мәніне әсер етпейді.

Мынаған назар аударған жөн, егер τ=0 болғанда ӨКФ-нің мәні максимумға жету тиіс емес.

Спектральді сипаттамалар арқыл екі сигналдық ӨКФ-н өрнектейік.

Рэлея формуласына негізделе отырып:

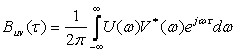аламыз.

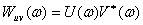шамасы сигналдың U(t) және V(t) өзара энергетикалық спектр екенін ескере отырып, шексіз жиіліктер интервалында -∞<ω<∞ анықталған, мынадай шешімге келеміз: Өзара корреляциялық функция және екі сигналдың өзара энергетикалық спектрі Фурье түрлендіруінің жұбымен байланысты.

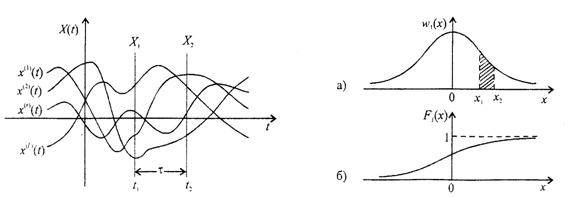
Жалпы байланыс теориясын зертттеу тәсілдерінің негізінде, уақыт бойынша дамитын кейбір кездейсоқ процесс ретіндегі хабарды тарату процессі жөніндегі көрсетілу жатыр. Кездейсоқ сөзі алдын-ала процестің нақты таралуын болжау мүмкін еместігін көрсетеді. Анықтау бойынша кездейсоқ процесс X(t)-бұл кез-келген t уақыт мезетінде қабылданатын мәндер кездейсоқ шамалар болып табылатын ерекше түрдегі функция. Кездейсоқ процесстің типтік мысалы ретінде қабылдағыш кірісінде Z(Q)=S(t)+N(t) кернеуі жұмыс жасай алады. Берілген мезетте кернеуді бақылай отырып, біз келесі уақыт мезеттерінде ол қандай мәнлерге ие бола алатындығын болжай аламыз. Бұл мынамен түсіндіріледі: таратушымен қалыптастырылатын арналық каналдың S(t) (амплитуда, жиілік, фаза) параметрлері жіберілетін хабарға a(t) байланысты кездейсоқ өзгеріп отырады. Сонымен бірге, таралу процесінде сигнал кездейсоқ сипатқа ие әртүрлі адетивті бөгеуілдердің N (t) әсеріне шалдығады. Мысалы: атмосфера электрлік разряд түрінде,электрлік транспорттың бөгеуілдері, басқа радиостанциялық бөгеуілдер және т.б. Процестің кездейсоқтылығы X(t) бақыланатын функцияның түрі бір бақылаудан басқасына кездейсоқ ауысатындығымен көрсетіледі. Бірақ, әрбір жеке тәжірибеден алынатын X(t) функцияның шешімі кездейсоқ емес, оны кездейсоқ функцияның таралуы(реализация)деп аталады. Кездейсоқ процесс статикалық ансамбль жасайтын шексіз мұндай таралулардың жиынтығын ұсынады. 5.1-суретте кездейсоқ процестің төрт таралуы көрсетілген. Егер графиктен кездейсоқ функцияның X (t) көптеген таралулар мезетін таңдасақ, онда көптеген таралу мәндері осы мезетте кездейсоқ шама құрайды. Бұл кездейсоқ шаманың мәндері алдын-ала белгісіз. Бірақ кейбір заңдылықтарды орнатуға болады. Бұл қимада кездейсоқ шама Р ықтималдықпен шектелген аралықтағы мәндерді қабылдайды.

Үзіліссіз процесстер X(t) үшін t,берілген қимасындағы ықтималдық тарауы бір өлшемді ықтималдық тығыздығымен сипатталады:

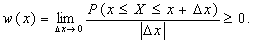
5.1 Сурет -Кездейсоқ процестің төрт тарлуы	5.2 Сурет -Бір өлшемді ықтималдық тығыздығының типтік графигі

Кездейсоқ шама X(t) аралындағы мәндерді қабылдайды. 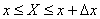аралығының шамасына 5.2 а суретте бір өлшемді ықтималдық тығыздығының типтік графигі көрсетілген.

Кездейсоқ шама (х₁;х₂) аралығында қандай да бір мәнге ие болу ықтималдығы 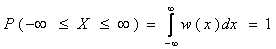өрнегімен анықталады.

Басқa х шамасынан асып кетпеу ықтималдығымен анықталатын кездейсоқ Х шамасының маңызды сипаттамасы ИФР F(x) болып табылады.

ИФР келесі қасиеттерге ие:

а ) F(-∞)=0;

б) F(∞)=1;

в) F(x) — шығынсыз функция, яғни х₂ > x₁ кезінде F (x₂) ≥ F (x₁);

г) P[x₁≤X≤x₂]=F(x₂)- F(x₁).

Қолданбалы есептерде ИФР дифференциалданатын функция деп есептелінеді және w(x) ИФР- ден алынған деп туынды деп анықтайды:

.

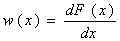Кездейсоқ процессті толығырақ сипаттау үшін кездейсоқ процесстің қасиетін сипаттайтын қималарында n - өлшемді ықтималдық тығыздығымен w(x₁, x_2,…, x_n; t₁,t_2,…, t_n) немесе F(x₁, x_2,…, x_n; t₁,t_2,…, t_n) n - өлшемді ИФР t₁,t_2,…, t_n бойынша орналыстыру керек.

Уақыт бойынша үзіліссіз СП-ні толық сипаттау үшін п→∞ ұмтылады. Процесс қималарда байқалатын кейбір мезеттер уақыттық аргументтерге тәуелді болады. Олар мезеттік функциялар деп аталады. Статикалық радиотехника үшін төменгі реттегі 3 мезеттік функциялардың маңызы зор. Олар: математикалық күтім, дисперсия және корреляция функциясы деп аталады.

6 Дәріс. Сигналдардың уақыт бойынша дискреттелуі

Дәрістің мазмұны:

- Үздіксіз функцияның лездік мәндерін дискретті санау кезегімен белгілеу. Санау теоремасы. Үздіксіз функцияның санақ боынша қалпына келтірілуі.

Дәрістің мақсаты:

- Шектелген спектрі бар сигналдың лездік мәндерінің неғұрлым дәл қалпына келтірілуінің мүмкіндігін бірдей уақыт аралығының есептік мәндері арқылы белгілеу.

Еркін үздіксіз функция 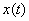ның дәл елестетілуі үшін соңғы уақыт интервалы 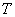да интервалдың барлық нүктелерінде, яғни бір бірінен шексіз аз интервада орналасқан үздіксіз есептеу көптігі арқылы лездік мәндер туралы деректерді басқару қажет. 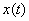функциясы туралы кейбір жақындатылған түсінікті оның интервалдарында санақ деп аталатын 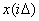мәндеріне ие дискретті импульс кезектері түріндегі бейнеленуі бойынша құруға болады.

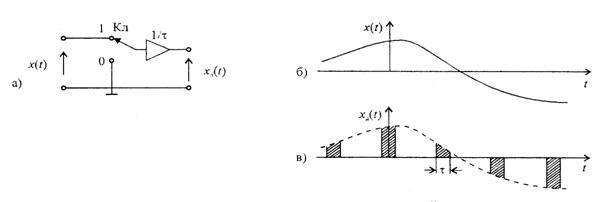
6.1 Сурет – Үздіксіз функцияның дискреттелу 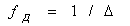жиілігі болатын периодикалық коммутацияның негізінде дискреттелуі

Үздіксіз функцияның оның лездік мәндерінің санау негізіндегі ауыстыруының амалы дискреттелу деп аталады. Дискреттелудің ең қарапайым физикалық моделі ретінде коммутациялық құрылғыны қарастырамыз. 6.1а суретінде көрсетілген Кл кілті көмегімен 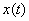үздіксіз сигналының көзіне дискреттелу жиілігі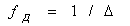, 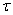уақыт бойынша периодтық қосылу орындалады, яғни 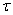интервалында 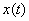қатарымен үздіксіз функцияның ауыстырылуы орындалады. 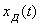санақтарының қатарын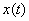 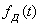периодтық импульстік дисткреттелу қатарына 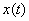туындысы ретінде есептеуге болады (6.2 суретті қара).

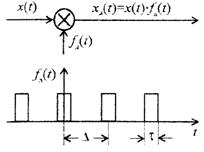
6.2 Сурет - x(t) үздіксіз функциясының оның периодтық қатарға көбейтілуі жолымен дискреттелуі

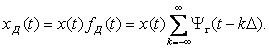
Мұндағы дискреттелу импульсі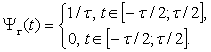

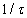көбейткіші 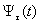функцияны бірлік ауданға келтіреді. Бұл үшін 6.1 а суреттің сызбасында Кл кілттен кейін масштабтық аудан енгізілген. x(t) Лездік мәндерінің 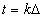нүктелеріндегі санақтарына өту үшін 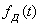периодтық функциясының 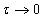кезіндегі ерекшеліктерін қарастыру қажет. 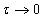кезінде бұл периодтық функция торлы функциямен 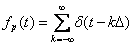алмастырылатынын байқау қиын емес. Дискретті сигнал .

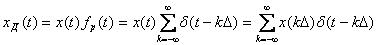Дата добавления: 2014-01-07