Разностное представление информации

При проведении опытов часто измеряемая величина имеет некоторое постоянное значение. Всякий раз при представлении отсчетами она записывается, хранится в памяти. Отсюда разностное представление основано на том, чтобы помнить (сохранять) изменения исследуемой величины (приращение).

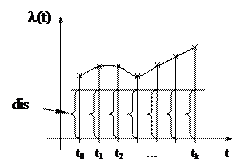
Рис.. Разностное представление информации.

Алгоритм получения разностного представления.

1. Измеряется вся координата (базовая точка) λ(t₀).

2. Измеряется координата в точке t₁, из которой вычитается базовая точка, получается приращение функции, это приращение и запоминается. Это простейшие разностные представления.

λ(t₁) – λ(t₀) = Δλ (t₁)

На практике применяют экстраполированное значение («угадывание»). На основании предыдущих 2 – 3 измерений вычисляется экстраполированное значение в следующей точке, пока мы еще не измерили ее, а значение уже экстраполировали λ₂(t₂).

Измерив, реальное значение находим разницу экстраполированного и реального значения Δλ_T = λ_э(t₂) – λ(t₂) и эту разницу помним.

Главная цель дифференциального представления – уменьшить число хранимых разрядов – тем самым, сократив объем требуемой памяти. Варианты разностного представления различны. На практике такую форму применяют в случае, когда объем хранимой информации должен быть малым. Однако такое сокращение хранит в себе высокую вероятность ошибки. Оттолкнувшись от базы следующее значение, мы как бы выстраиваем на основе предыдущего, и если какое-либо предыдущее оказалась с ошибкой, то все последующие несут в себе эту ошибку. Основная ошибка представления – погрешность по наклону.

При получении разности Δλ абсолютное значение не укладывается в отведенную разрядную сетку, т.е. число столь большое, что разрядов не хватает. Например, n = 6 0÷63 0,03

Суммарная погрешность представления разностного объединяется их четырех составляющих

S_р∑ = S_пр + S_кв + δ_ПН + δ_АН

– две составляющих предыдущего исполнения – преобразования и квантования

– две других составляющих δ_ПН – погрешность по наклону и δ_АН – аномальная – случайная составляющая, определяемая шумами в блоках (вычитатели, экстраполяция).

На практике чаще всего применяют представления отсчетами в силу меньшей погрешности и большей логичности результата. АЦП основаны на представлении отсчетами.

3. Интегральное представление информации

Третьим видом представления информации считают интегральное. Первоначально получают массив отсчетов. Получив массив, проводят преобразование чисел в их описание – заменяют функцией. Для этого применяют кусочное разбиение и представляют на каждом участке своим полиномом. Результат хранят в форме коэффициентов полинома и вид полинома (квадратичный, линейный). Это приводит к значительному сокращению объема памяти. Интегральное представление используют для обработки результатов опытов, т.е. после опытов текущее значение этой формы не представляют.

Оптимальное представление информации

Любую непрерывную величину можно измерять с различной частостью, интервал 1 минута, 1 час. Оптимальным считают такое измерение, объем информации при котором наименьший, но величина погрешности измерения ≤ допустимого значения.

I_изм→ I_min; δ_∑ ≤ δ_доп δ_∑ = δ_доп

Теорема Котельникова определяет условие оптимальности. Если интервал дискретизации будет равен дроби это точка оптимума. На практике все же Δt несколько меньше по техническим причинам.

Δt = 1/2f_в Δt ≤ 2f_в

Таким образом, сигнал при дискретизации - объем получения информации очень зависит от ширины спектра измеряемого сигнала. Чем сложнее сигнал, тем быстрее его нужно измерять, чтобы сохранить все характеристики.

Формула Котельникова учитывает максимальную верхнюю частоту спектра на неопределенном интервале. В то же время часто встречаются, переходные процессы в электрических цепях, которые имеют различную спектральную плотность во времени.

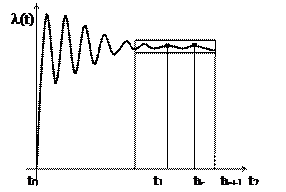
Рис..Переходной процесс с различной

спектральной плотностью во времени.

Интервал t₀ – t₁ – непосредственно затухающее колебание, имеет широкий спектр в то время, как от t₁ до t₂ спектр значительно сокращается. Формально мы должны анализировать весь интервал t₀ – t₂ и соответственно учитывать самый широкий спектр. На практике подобные процессы анализируются по адаптивным алгоритмам, измеряющим какой-либо параметр.

Адаптация по временному интервалу.

Для снижения (минимизации) объема хранимой информации применяют адаптацию по временному интервалу.

1) по теореме Котельникова анализируют

Δ t_min ≤ 1/2f_в

2) начинают измерять в точке t₀; (t₀ + Δt_min)

3) сравнивают разность λ(t₀) – λ(t₁); если эта разность больше ε, то запоминают значение в этой точке→ помнить λ(t₁).

ε ≈δ_доп/2

4) λ(t₁) – λ(t₂) >ε → запомнить.

Рис.. Адаптация по временному интервалу.

Пока идет быстрое изменение величины в память посылаются все измеренные значения параметра. Графически это можно представить: вверх и вниз откладывается апертура ε, и если предыдущее значение точки не попало в апертуру, то новая координата запоминается. Когда функция стабилизируется, последующие значения попадают в область апертуры и нет необходимости запоминать координаты последующих точек. Мы помним лишь ту последнюю координату, с которой начиналось совпадение.

Чтобы масштаб функции не изменился, вводят счетчик числа пропущенных точек. Каждая пропущенная координата добавляет 1 в счетчик, таким образом, данный алгоритм при быстрых изменениях записывает в память все значения, при медленном изменении функции – только те, которые отличаются на апертуру и более. Фактически получается, что время измерения переменное.

Дата добавления: 2014-01-07