Векторы. Линейные операции над векторами

Вектор. Длина вектора. Вектором называется направленный отрезок. Вектор характеризуется двумя величинами: длиной и направлением. Также вектор можно задать указав его начало и конец. Векторы обозначают следующим образом: AB,`a.

Вектор начало и конец, которого совпадают, называется нулевым. Векторы ` а и `в называются коллинеарным, если они лежат на одной прямой или на параллельных прямых.

Векторы ` а и называются равными, если они коллинеарны, одинаково направлены и их длины равны.

Если вектор задан началом А(х₁,у₁) и концом В(х₂;у₂), то координаты вектора АВ можно определить так АВ

Длина вектора АВ определяется как расстояние между двумя точками:

(1)

Пусть задана ось И и некоторый вектор АВ. Проекцией вектора АВ на ось И называется величина А¢В¢ на оси И. Проекция вектора АВ на ось И равна длине вектора АВ, умноженной на косинус угла между вектором АВ и осью И, т.е.

Пр_и (2)

Направляющими косинусами вектора ` а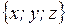 называются косинусы углов между вектором ` а и осями координат. Направляющие косинусы вектора `а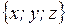можно определить по формулам

Векторы можно складывать, вычитать и умножать на число.

Определение 1. Суммой называется вектор, который идет из начала вектора в конец вектора при условий, что вектор приложен к концу вектора .

Определение 2. Разностью 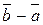векторов и называется вектор, который в сумме с вектором дает вектор .

Определение 3. Произведением 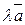называется вектор, который коллинеарен вектору , имеет длину, равную и направление такое же, как и вектор , если >0 и противоположное, если <0.

Пусть даны векторы 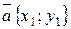и . Тогда сумма векторов в координатной форме записывается

,

разность векторов

,

умножение вектора на число l

.

Нелиейные операции над векторами. Метод координат

Скалярным произведением двух векторов 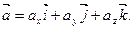и называется число, определяемое равенством

.

Свойства скалярного произведения векторов:

. (переместительное свойство)

.

.

.

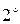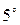. , если

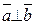
Векторным произведением двух векторов 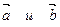называется вектор, длина которого равна

,где 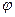- угол между

векторами .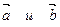

И который направлен перпендикулярно

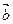векторам 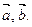Векторы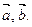 образуют

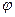так называемую правую тройку.

Рис. 1

Вектор находится по формуле:

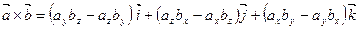(5)

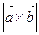Геометрически равна площади параллелограмма, построенного на векторах

Смешанное произведение векторов 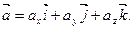, , 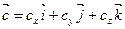есть число, определяемое формулой:

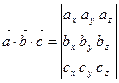
Модуль 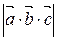смешанного произведения равен объёму параллелепипеда, построенного на векторах

Метод координат.

Аналитическая геометрия изучает геометрические образы алгебраическими методами. Аппаратом аналитической геометрии является метод координат, разработанный Декартом в XVII веке. В основе метода координат лежит понятие системы координат.

Две взаимно перпендикулярные оси О_х и О_у, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат. Ось О_х называется осью абсцисс, ось О_у – осью ординат.

В прямоугольной системе координат О_ху точку М, имеющую координаты х и у, обозначают М(х; у), где х – абсцисса точки, а у – её ордината.

Пусть в прямоугольной системе координат заданы точки М₁(х_1, у₁) и М₂(х₂;у₂). Расстояние между ними определяется по формуле:

(1)

Три точки плоскости, не лежащие на одной прямой образуют треугольник.

Теорема. Для любых трех точек А(х₁;у₁),В(х₂;у₂) и С(х₃;у₃), не лежащих на одной прямой, площадь S треугольника АВС вычисляется по формуле

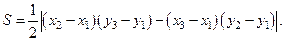(2)

Пусть на плоскости дан произвольный отрезок М₁М₂ и пусть М – любая точка этого отрезка, отличная от точки М₂.

Координаты точки М(х;у) делящей отрезок между точками М₁(х₁;у₁) и М₂(х₂;у₂) в заданном отношении λ, определяются по формулам:

(3)

При λ=1 получаем формулы для координат середины отрезка:

(4)

В полярной системе координат положение точки М на плоскости определяется её расстоянием |ОМ|=ρ от полюса О (ρ –полярный радиус-вектор точки) и углом φ, образованным отрезком ОМ с полярной осью ОЕ Угол φ считается положительным при отсчете от полярной оси против часовой стрелки.

Прямоугольные координаты х и у точки М и её полярные координаты ρ и φ связаны следующими формулами

Лекция 4

Дата добавления: 2014-01-07