
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная. Правила и формулы дифференцирования
|
|
|
|
Напомним, что приращением функции у = f (х) называется разность 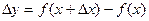 , где
, где 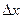 - приращение аргумента х.
- приращение аргумента х.
Из рисунка видно, что 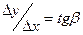 (1).
(1).
Предел отношения приращения функции 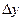 к приращению аргумента
к приращению аргумента 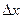 при произвольном стремлении
при произвольном стремлении 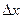 к нулю называется производной функции у=f (х)в точке х и обозначается одним из следующих символов: у ', f '(х),
к нулю называется производной функции у=f (х)в точке х и обозначается одним из следующих символов: у ', f '(х), 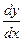 .
.
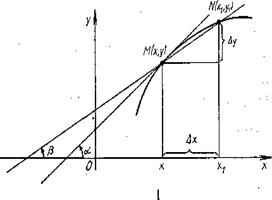
Рис. 1.
Таким образом, по определению
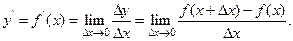 (2)
(2)
Если указанный в формуле (2) предел существует, то функцию f (х) называют дифференцируемой в точке х, а операцию нахождения производной у ' – дифференцированием.
Из равенства (1) и определения производной, (см. формулу (2)) следует, что производная в точке х равна тангенсу угла 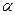 наклона касательной, проведенной в точке М (х, у), к графику функции у = f (х) (см. рис. 1).
наклона касательной, проведенной в точке М (х, у), к графику функции у = f (х) (см. рис. 1).
Легко показать, что с физической точки зрения производная у '= f '(х) определяет скорость изменения функции в точке х относительно аргумента х.
Если С — постоянное число и и=и(х), v=v (x) – некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (С)'=0;
2) (х)'.=1;
3) (и 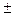 v)'= и '
v)'= и '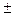 v ';
v ';
4) (С и)'= С и '
5) (и v) '=и' v+иv';
6) 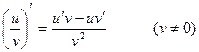 ;
;
7) 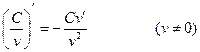 ;
;
8) если у = f (и) и u =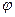 (х), т. Е. y = f (
(х), т. Е. y = f (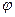 (x)) – сложная функция, составленная из дифференцируемых функций, то
(x)) – сложная функция, составленная из дифференцируемых функций, то
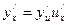 или
или 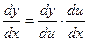 ;
;
9) если для функции у = f (х) существует обратная дифференцируемая функция х=g(у) и 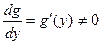 , то f '(х) =
, то f '(х) =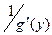 .
.
На основании определения производной и правил дифференцирования можно составить таблицу производных основных элементарных функций:
1) 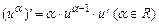
| 2) (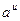 )' = )' = 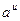 lnа•u' lnа•u'
|
| 3) (е u)'=е u u ' | 4) 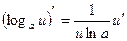
|
5) 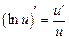
| 6) (sin u)’= соs uu ’ |
| 7) (соs u)’=-sin u u ’ | 8) 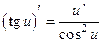
|
9) 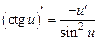 ; ;
| 10) (arcsin u)'=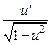
|
11) 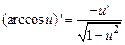
| 12) 
|
13) 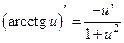
|
Уравнение касательной к кривой у = f (х) в точке М о(х 0; f(х 0))
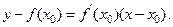
Уравнениe нормали к кривой у = f (х) в точке М о(х 0; f (х 0)):
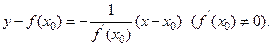
При f /(х 0)=0 уравнение нормали имеет вид х = х 0.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым в этой точке.
Логарифмической производной функции у = f (х) называется производная от логарифма этой функции, т. Е.
(ln f (x))’= f ’(x)/ f (x).
Последовательное применение логарифмирования и дифференцирования функций называют логарифмическим дифференцированием. В некоторых случаях предварительное логарифмирование функции упрощает нахождение ее производной. Например, при нахождении производной функции у=иv, где и=u(х), v=v(х), предварительное логарифмирование приводит к формуле
у =иv ln и v' + v и v -1 и'.
Если зависимость между переменными у и х задана в неявном виде уравнением F (х, у)=0, то для нахождения производной у' =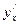 в простейших случаях достаточно продифференцировать обе части уравнения F (х, у)=0, считая у функцией от х, и из полученного уравнения, линейного относительно у ', найти производную.
в простейших случаях достаточно продифференцировать обе части уравнения F (х, у)=0, считая у функцией от х, и из полученного уравнения, линейного относительно у ', найти производную.
Производные высших порядков. Дифференциалы первого и высших порядков и их приложения.
Производной второго порядка или второй производной функции у = f (х) называется производная от ее первой производной, т. Е. (у ')'. Обозначается вторая производная одним из следующих символов: у», f ''(х), 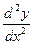 .
.
Если s = s (t) – закон прямолинейного движения материальной точки, то s '=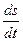 - скорость, а s»=
- скорость, а s»= - ускорение этой точки.
- ускорение этой точки.
Если зависимость функции у от аргумента х задана в параметрическом виде уравнениями х = х(t), у=у(t), то:
 (3)
(3)
где штрих обозначает производную по t.
Производной n -го порядка функции у=t(х) называется производная от производной (n -1)-го порядка данной функции. Для n -й производной употребляются следующие обозначения: у(n), f (n) (х), 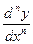 . Таким образом,
. Таким образом,
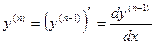 .
.
Дифференциалом первого порядка функции у = f (x) называется главная, часть ее приращения, линейно зависящая от приращения 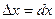 независимой переменной х. Дифференциал
независимой переменной х. Дифференциал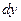 функции равен произведению ее производной и дифференциала независимой переменной
функции равен произведению ее производной и дифференциала независимой переменной 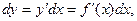 поэтому –справедливо равенство
поэтому –справедливо равенство 
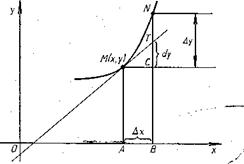 Из рисунка видно, что если МN - дуга графика функции
Из рисунка видно, что если МN - дуга графика функции 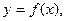 МТ – касательная, проведенная к нему в точке М (х, у), и
МТ – касательная, проведенная к нему в точке М (х, у), и 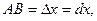 то CT = dy, а отрезок
то CT = dy, а отрезок  Дифференциал функции dy о
Дифференциал функции dy о тличается от ее приращения
тличается от ее приращения 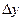 на бесконечно малую высшего порядка по сравнению с
на бесконечно малую высшего порядка по сравнению с 
Непосредственно из определения дифференциала и правил нахождения производных имеем:
1) 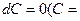
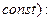

2) 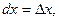 если х – независимая переменная;
если х – независимая переменная;
3) 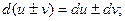
4) 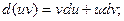
5) 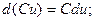
6) 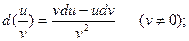

7) 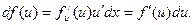
Дифференциалом n -го порядка функции у = f (х) называется дифференциал от дифференциала (n -1)-го порядка этой функции, т. Е. dny = d (dn -1 y).
Если дана функция у=f (х), где х – независимая переменная, то d2у= у»dх2, d3у=у'»dх3, …, dnу= y(n)dxn.
Если у=f (u), где u=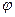 (x), то d2y=y//(du)2+y/d2u, где дифференцирование функции y выполняется по переменной и. (Это имеет место и для дифференциалов более высоких порядков.)
(x), то d2y=y//(du)2+y/d2u, где дифференцирование функции y выполняется по переменной и. (Это имеет место и для дифференциалов более высоких порядков.)
Так как дифференциал функции отличается от ее приращения на бесконечно малую величину высшего порядка по сравнению с величиной dх, то 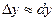 или
или 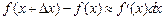 , откуда
, откуда 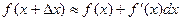 .
.
Полученная формула часто применяется для приближенного вычисления значений функции при малом приращении 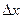 независимой переменной х.
независимой переменной х.
С помощью дифференциала функции вычисляют абсолютную погрешность функции 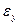 , если известна абсолютная погрешность
, если известна абсолютная погрешность 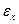 аргумента. В практических задачах значения аргумента находятся с помощью измерений, и его абсолютная погрешность считается известной.
аргумента. В практических задачах значения аргумента находятся с помощью измерений, и его абсолютная погрешность считается известной.
Пусть требуется вычислить значение функции у = f (х) при некотором значении аргумента х, истинная величина которого нам неизвестна, но дано его приближенное значение x 0 с абсолютной погрешностью 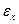 : х= x 0+ dх,
: х= x 0+ dх, 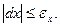 Тогда
Тогда
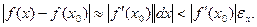
Отсюда видно, что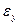 =
=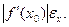 Относительная погрешность функции
Относительная погрешность функции  выражается формулой
выражается формулой
 =
=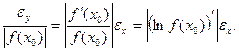
Лекция 18
Основные теоремы дифференциального исчисления (Ферма,
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 370; Нарушение авторских прав?; Мы поможем в написании вашей работы!