Ролля, Лагранжа, Коши). Правило Лопиталя

Приложения производной и исследование функции.

Теорема 1 (Ферма). Если функция у=f (x) достигает своего наибольшего или наименьшего значения в точке с из интервала (a; b) и дифференцируема в этой точке, тогда

Теорема 2 (Ролля). Если функция у=f (x) непрерывна на отрезке [ a; b ], дифференцируема внутри этого отрезка и f (a)= f (b), то существует по крайней мере одна точка с (a < c < b) такая, что f ^/(c)=0.

Теорема 3 (Лагранжа). Если функция непрерывна на отрезке и дифференцируема внутри этого отрезка, то существует по крайней мере одна точка такая, что

Эта формула называется формулой Лагранжа конечных приращений.

Теорема 4 (Коши). Если функции и 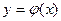непрерывны отрезке и дифференцируемы внутри него, причем нигде при то найдется хотя бы одна точка такая, что

Правило Лопиталя (для раскрытия неопределенностей вида ). Если функции удовлетворяют условиям теоремы Коши в некоторой окрестности точки х = х ₀, стремятся к нулю (или при 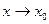и существует То существует также и эти пределы равны, т.е.

Правило Лопиталя справедливо и при Если частное 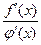вновь дает в предельной точке неопределенность одного из двух названных видов и функции 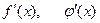удовлетворяют всем требованиям, ранее указанным для функций то можно перейти к отношению вторых производных и т. Д. Однако следует помнить, что предел отношения самих функций может существовать, в то время как отношение производных не стремится ни к какому пределу.

Лекция 19.

Дата добавления: 2014-01-07