Числовые ряды

Пусть дана числовая последовательность .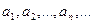

Выражение вида 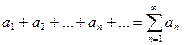называется числовым рядом или просто рядом.

При этом числа 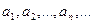называются членами ряда, а член 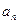с произвольным номером — общим членом ряда.

Суммы конечного числа членов ряда:

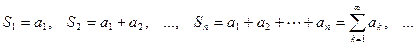
называются частичными суммами ряда. Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм .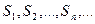

Если все члены ряда положительны, то ряд называется знакоположительным.

Ряд называется сходящимся, если предел 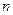-частичной суммы существует и конечен, т.е. 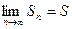, в противном случае говорят, что ряд расходится. При этом 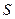называется суммой ряда.

Ряд: ,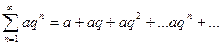

где 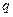- знаменатель геометрической прогрессии, называется рядом геометрической прогрессии.

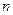-частичная сумма ряда геометрической прогрессии равна:

= .

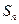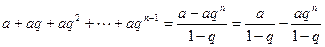Ряд геометрической прогрессии является сходящимся при 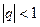(его сумма 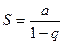) ирасходящимся при .

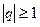Свойства сходящихся рядов:

6. Если сходится ряд:

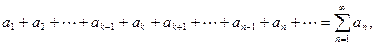
то сходится и ряд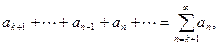

и обратно, если сходится второй ряд, то сходится и первый.

Другими словами, на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.

2) Если ряд 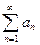сходится и его сумма равна 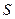, то и ряд 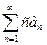, где с — некоторое число, также сходится, и его сумма равна .

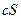7. Если ряды 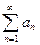и 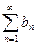сходятся и их суммы соответственно равны 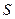и 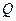, то и ряд 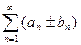cходится и его сумма равна .

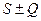Таким образом, установлено, что сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы.

Необходимое и достаточные условия сходимости ряда.

При рассмотрении рядов возникают две задачи: 1) исследовать ряд на сходимость и 2) зная, что ряд сходится, найти его сумму. Будем решать в основном первую задачу, имеющую теоретический характер. Приведем необходимое условие сходимости рядов.

Если ряд 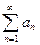сходится, то его общий член стремится к нулю, т.е. 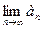=0.

Числовой ряд:

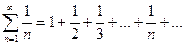
называется гармоническим рядом.

Только невыполнение необходимого условия сходимости позволяет делать определённый вывод, а его выполненине, как в данном случае 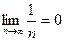, не позволяет судить о сходимости.

Лекция 42

Дата добавления: 2014-01-07