
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные дифференциальные уравнения второго порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
|
|
|
|
Уравнение вида:
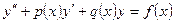 ,
,
где 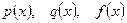 - заданные непрерывные функции от х, называется линейным неоднородным дифференциальным уравнением второго порядка, а соответствующее ему уравнение:
- заданные непрерывные функции от х, называется линейным неоднородным дифференциальным уравнением второго порядка, а соответствующее ему уравнение:
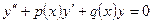
- линейным однородным.
Если 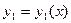 и
и  - какие-нибудь два линейно независимых частных решения однородного дифференциального уравнения второго порядка, то его общим решением служит функция:
- какие-нибудь два линейно независимых частных решения однородного дифференциального уравнения второго порядка, то его общим решением служит функция:
 .
.
Функции 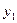 и
и  называются линейно независимыми, если при постоянных
называются линейно независимыми, если при постоянных 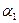 и
и  тождество
тождество  выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 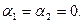 Если же хотя бы одна из них отлична от нуля, а тождество
Если же хотя бы одна из них отлична от нуля, а тождество  возможно, то эти решения
возможно, то эти решения 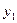 и
и  называются линейно зависимыми.
называются линейно зависимыми.
Общее решение линейного неоднородного дифференциального уравнения второго порядка есть сумма его частного решения и общего решения соответствующего ему линейного однородного дифференциального уравнения:
 ,
,
где  - частное решение неоднородного, а
- частное решение неоднородного, а 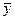 - общее решение однородного уравнения.
- общее решение однородного уравнения.
Пусть требуется решить линейное однородное дифференциальное уравнение второго порядка:
 ,
,
в котором  и
и 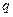 - постоянные величины.
- постоянные величины.
Найдём частные решения дифференциального уравнения в виде 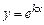 . Тогда
. Тогда 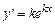 ,
,  . Подставив выражения
. Подставив выражения 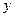 ,
, 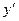 и
и  в исходное уравнение, получим:
в исходное уравнение, получим:
 .
.
Так как 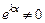 , то получим уравнение
, то получим уравнение
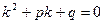 ,
,
которое называется характеристическим уравнением линейного однородного дифференциального уравнения второго порядка.
Таким образом, 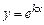 является частным решением линейного однородного дифференциального уравнения второго порядка, если
является частным решением линейного однородного дифференциального уравнения второго порядка, если 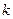 - корень характеристического уравнения.
- корень характеристического уравнения.
В зависимости от дискриминанта корни характеристического уравнения могут быть:
1) действительными и различными 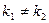 , тогда частные решения
, тогда частные решения 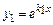 и
и  , а общее решение:
, а общее решение:
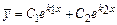 ,
,
2) действительными и равными  , тогда частные решения
, тогда частные решения 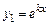 и
и 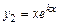 , а общее решение:
, а общее решение:
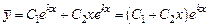 ,
,
4. комплексными  ,
,  , тогда частные решения
, тогда частные решения  и
и  , а общее решение:
, а общее решение:
 .
.
Общее решение линейного неоднородного дифференциального уравнения второго порядка:
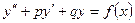 ,
,
в котором  и
и 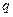 - постоянные величины, находится как:
- постоянные величины, находится как:
 ,
,
где  - частное решение неоднородного, а
- частное решение неоднородного, а 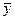 - общее решение однородного уравнения.
- общее решение однородного уравнения.
 ,
,
Общее решение однородного уравнения, как известно, находится с помощью характеристического уравнения, а частное решение неоднородного уравнения находится в зависимости от вида функции 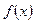 .
.
5. Если  есть многочлен
есть многочлен 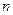 -ой степени:
-ой степени:
 ,
,
в частности, многочлен второй степени  (
( ), то частное решение неоднородного уравнения ищется в виде:
), то частное решение неоднородного уравнения ищется в виде:
а) 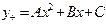 при
при 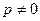 и
и 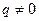 ;
;
б)  при
при 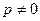 и
и 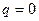 ;
;
в) при  и
и 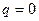 неоднородное дифференциальное уравнение принимает вид:
неоднородное дифференциальное уравнение принимает вид: 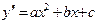 , решение которого находится непосредственным двукратным интегрированием, т.е.
, решение которого находится непосредственным двукратным интегрированием, т.е. 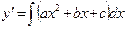 , затем,
, затем,  .
.
2. Если 
 - показательная функция, т.е.
- показательная функция, т.е.  (
( ), то частное решение неоднородного уравнения ищется в виде:
), то частное решение неоднородного уравнения ищется в виде:
а) 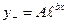 , если коэффициент
, если коэффициент  не является корнем характеристического уравнения, т.е.
не является корнем характеристического уравнения, т.е. 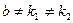 ;
;
б)  , если коэффициент
, если коэффициент  является однократным корнем характеристического уравнения, т.е.
является однократным корнем характеристического уравнения, т.е.  ;
;
в)  , если коэффициент
, если коэффициент  является двукратным корнем характеристического уравнения, т.е.
является двукратным корнем характеристического уравнения, т.е.  .
.
3. Если  - тригонометрическая функция, т.е.
- тригонометрическая функция, т.е. 
 , то частное решение неоднородного уравнения ищется в виде:
, то частное решение неоднородного уравнения ищется в виде:
а) 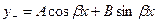 , если
, если 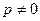 ;
;
б) 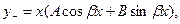 если
если  , а
, а  .
.
Лекция 41.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 368; Нарушение авторских прав?; Мы поможем в написании вашей работы!