Частные производные и дифференциалы высших порядков. Теорема о равенстве смешанных частных производных

Пусть функция 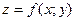дифференцируема в области и ее частные производные первого порядка сами являются функциями двух переменных.

Определение. Частная производная от частной производной первого порядка называется частной производной второго порядка.

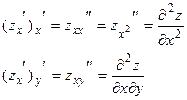
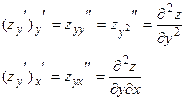
Определение. Частными производными 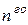порядка называются частные производные от частных производных 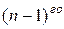порядка.

Определение. Частные производные по различным переменным называется смешанными. Их обозначают , …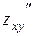

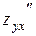Теорема. Если смешанные производные существуют и непрерывны, то они равны между собой, то есть .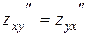

Пример.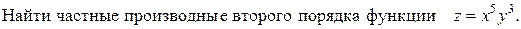

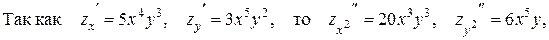
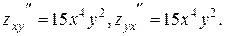
Определение. Полным дифференциалом второго порядка функции 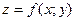называется ее полный дифференциал от полного дифференциала первого порядка.

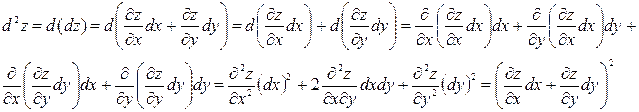
Определение. Полным дифференциалом 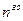порядка функции двух переменных 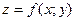называется ее полный дифференциал от полного дифференциала 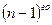порядка и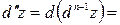

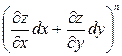
Дата добавления: 2014-01-07