Теорема Абеля. Радиус сходимости степенного ряда. Дифференцирование и интегрирование степенных рядов

Теорема (Абеля). Если степенной ряд (3) сходится в точке 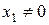, то он

сходится абсолютно при всех . Если степенной ряд расходится в

точке 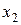, то он расходится при всех .

Из теоремы Абеля вытекает, что область сходимости степенного ряда есть некоторый, симметричный относительно центра, промежуток.

Определение. Число R называется радиусом сходимости степенного ряда,

если степенной ряд (3) сходится для каждого и расходится для всех .

Для степенных рядов возможны три случая:

1) При R =0 ряд (3) сходится в единственной точке x =0. При каждом ряд расходится.

2) При ряд (3) сходится на всей числовой оси.

3) При 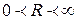ряд сходится для всех и расходится при . На концах интервала в точках x=-R и x=R степенной ряд может либо сходиться, либо расходиться. Эти точки дополнительного исследования.

Радиус сходимости ряда (3) определяется по формулам

или .

Теорема. Степенной ряд внутри интервала сходимости можно почленно дифференцировать и интегрировать, при этом радиус сходимости ряда не меняется. Вновь полученные ряды сходятся абсолютно на (-R;R).

Замечание. Сходимость ряда может измениться на концах интервала сходимости.

Дата добавления: 2014-01-07