
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Необходимые сведения из теории информации
|
|
|
|
Методы информационного описания погрешностей средств и результатов измерений
Теория информации является дальнейшим развитием теории вероятностей применительно к процессам получения и передачи информации и, в частности, к процессам измерения. “Основная идея теории информации, – писал К.Шеннон, – состоит в том, что с информацией можно обращаться почти так же, как с физическими величинами…”. Но “почти также” не означает “точно также”. Как утверждал Н.Винер, “Информация есть информация, а не вещество и не энергия”. Поэтому для однозначной характеристики процессов передачи информации существует особый функционал.
Это следует из того, что СКО s, явилась энергетической оценкой, т.е. оценкой мощности помехи, не определяет однозначно ее мешающего, дезинформирующего влияния. Анализ дезинформирующего действия случайных помех с разными законами распределения вероятностей привел К.Шеннона к выводу, что вносимая помехой дезинформация определяется не только мощностью этой помехи, т.е. ее СКО s, но еще зависит от вида закона распределения этой помехи. При этом, если помеха в вероятном смысле не зависит от сигнала, то дезинформационные действия помехи определяются ее энтропией
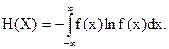
Информационное описание измерения заключается в следующем. Согласно К.Шеннону, количество информации I определяется как разность энтропий:
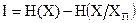 ,
,
где 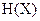 – энтропия (мера неопределенности) измеряемой величины до ее измерения, а
– энтропия (мера неопределенности) измеряемой величины до ее измерения, а 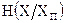 (энтропия X при условии XП) – энтропия действительного значения X измеряемой величины (мера интервала неопределенности) вокруг полученного после измерения показания XП, т.е. энтропия погрешности измерения. Эти оценки неопределенности в виде энтропии до и после измерения могут быть вычислены на основании вероятностного описания ситуации до и после измерений.
(энтропия X при условии XП) – энтропия действительного значения X измеряемой величины (мера интервала неопределенности) вокруг полученного после измерения показания XП, т.е. энтропия погрешности измерения. Эти оценки неопределенности в виде энтропии до и после измерения могут быть вычислены на основании вероятностного описания ситуации до и после измерений.
Допустим, для измерения величины X был использован прибор со шкалой от X1 до X2 (например, для измерения напряжения – вольтметр со шкалой от 0 до 100 В). тогда вероятностное описание ситуации до измерения состоит в том, что вероятность получить показания прибора в интервале от -¥ до X1 и от X2 до +¥ равна нулю, т.е. плотность вероятности f(х) в этих интервалах также равна нулю. Следовательно, показание можно ожидать лишь в интервале от X1 до X2 и, если предположить, что оно с равной вероятностью может оказаться в любой части диапазона, то вероятностное описание ситуации до измерения изобразится равномерным распределением X в пределах от X1 до Х2 и может быть записано
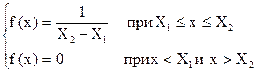
Отсюда энтропия до измерения будет равна
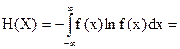
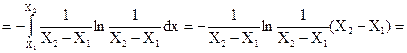
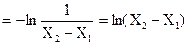
Следовательно, энтропия до измерения есть логарифмическая мера длины этого интервала (т.е. диапазона измерения прибора).
После проведения измерения мы получаем отчет ХП. Однако прибор имеет абсолютную погрешность ±D. Следовательно действительное значение измеряемой величины лежит в пределах нового интервала неопределенности ±D, т.е. шириной d=2D. Погрешность распределена по какому-либо закону. Допустим, что распределение погрешности имеет равномерный закон (рис. 1.19.). Тогда ситуация после измерения описывается распределением шириной d=2D и плотностью f(D)=1/2D.
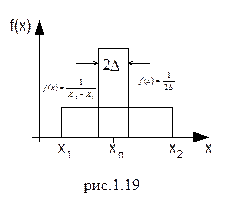 |
Таким образом, в понятиях теории информации смысл измерения состоит в сужении интервала неопределенности от
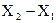 до измерения до
до измерения до 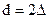 после измерения, т.е.
после измерения, т.е. 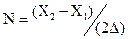 раз.
раз.
Энтропия результата измерения после получения результата Хn будет равна
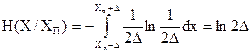 ,
,
т.е. тоже является логарифмической мерой неопределенности.
Количество информации, полученное в результате измерения
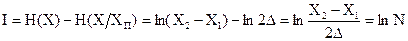 . Очевидно, что N показывает, сколько интервалов неопределенности d укладывается во всем диапазоне измерения прибора X2-X1, т.е. какое число различимых градаций измеряемой величины позволяет получить данный прибор.
. Очевидно, что N показывает, сколько интервалов неопределенности d укладывается во всем диапазоне измерения прибора X2-X1, т.е. какое число различимых градаций измеряемой величины позволяет получить данный прибор.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 301; Нарушение авторских прав?; Мы поможем в написании вашей работы!