Задачи о выборе оптимальных технологий

Пусть при производстве какого-либо продукта используется n -технологий, при этом требуется m-видов ресурсов, заданных объемом b_i (1; n).Эффективность технологий определяет количество конечной продукции (руб.), производимой в единицу времени по j технологии(1; n).Обозначим эффективность c_j. Коэффициент a_ij – расход i- ресурса в единицу времени по j- технологии. х_j – интенсивность используется j- технологии, т.е. это время, в течение которого продукты производятся по j- технологии. Необходимо найти план интенсивностей использования технологий, обеспечивающий максимум выпуска продукции в стоимостном выражении.

Max Z = 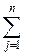c _j x _j

B _i => a _ij x _j

x _j =>0

Задача о диете.

Имеется n- пищевых продуктов, они содержат питательные вещества, обозначаемые 1,2,3,.., m. Единица j –продукта содержит a _ij единиц i –питательного вещества. Для нормальной жизнедеятельности в заданный промежуток времени необходимо потреблять не менее b_i единиц i – питательного вещества. c_j –стоимость единицы продукта j – вида. Требуется выбрать рацион минимальной стоимости, содержащих необходимое количество питательных веществ. План задачи (х) – это количество x_j, обеспечивающих необходимое количество питательных веществ, при минимуме затрат на исходные продукты.

Min Z = 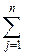c _j x _j

x _j =>0.

B _i <= 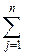a _ij x _j

Транспортная задача.

Рациональной перевозки некоторого продукта от производителей к потребителю. При этом имеется баланс между суммарным спросом потребителя и возможностями поставщиков по их удовлетворению. Потребителям безразлично из каких пунктов будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Задача о более рациональном прикреплении потребителя к поставщикам, правильном направлении перевозок груза, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, затраты на транспорт минимальны.

Имеется m-пунктов производства, в каждом из которых сосредоточено a_i, где i =(1 ;m) единица однородного продукта. Этот продукт необходимо доставить n –потребителям, где потребность b_i. c_ij – это затраты на перевозку единицы продукта из i –пункта производства в j –пункт потребителя. х_ij – количество продукта, перевозимые из i –пункта производства в j –пункт потребителя. Составляем макет.

Bi, a i	B1	B 2	…	bn
A 1	C11   X11	C12   X12	…	C1n   X1n
A2	C21   X21	C22   X22	…	C2n   X2n
…	…	…	…	….
a m	Cm1     Xm1	Cm2     Xm2	…	C mn     Xmn

Целевая функция минимальна при следующих ограничениях:

1) на возможности поставщиков весь продукт из пунктов производства должен быть вывезен.

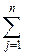x _ij = a _i

2) ограничение на спрос потребителей, который должен быть удовлетворен.

B _I = 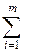x _ij

3) ограничение неотрицательности.

Дата добавления: 2014-01-07