Геометрическая интерпретация и графические решения задач линейного программирования

Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и исследовать даже смежные свойства.

Задачи линейного программирования с двумя переменными может решаться группами. Однако еще в трехмерном пространстве такое решение усложняется.

1)область допустимых решений – выпуклый многоугольник

2)неограниченная выпуклая область многоугольная

3)одна точка

4)линия

5)луч

6)решение на отрезке

7)пустое множество

Пусть область допустимых решений не пустое множество, например, некий многоугольник. Выберем произвольное значение функции Z = Z₀ следовательно Z₀ = c₁x₁ + c₂x₂.

В точках N и M целевая функция сохранит постоянное значение Z. Считая Z параметром, получим уравнение семейства параллельных прямых, называемых линиями уравнения целевой функции(линиями постоянного значения).Когда направление уменьшается или увеличивается, то целевая функция находится с помощью частных производных. Частные производные показывают скорость увеличения функции вдоль заданной оси следовательно, c₁ и c₂ скорость увеличения функции Z вдоль Ox₁ и Ox₂. c – это вектор, вектор градиент показывает направление наискорейшего увеличения целевой функции.

Порядок графического решения задач:

1)с учетом системы ограничений строится область допустимых значений.

2)строим вектор с

3)проводим произвольную линию уровню Z = Z₀

4)при решении задач на max перемещая линию уровня Z = Z₀ в направлении вектора с так, чтобы она касалась области дополнительных решений в ее крайнем положении (А₄ – максимальное значение). при решении на min –в антиградиентном направлении.(А₁).

5)оптимальный план х* и экстремальное значение целевой функции Zx*, где х – * это набор значений.

А) оптимальный план здесь единственный, линия уровня и область допустимых решений в разрешенных положениях имеют одну точку.

Б) бесконечное множество

В) Z стремится к бесконечности

Г) точка, Z как max так и min

Д) пустое множество

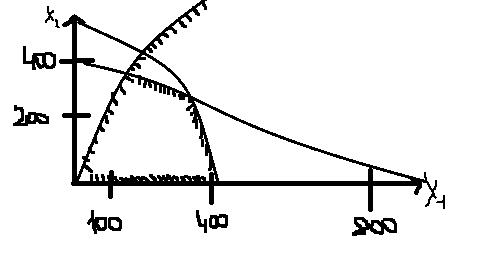
Пример задачи: цех выпускает 2 вида продукции, используя 2 вида полуфабрикат. Продукция используется при комплектовании изделий, при этом на каждую единицу продукции первого вида требуется не более двух единиц продукции второго вида. Нормой расхода полуфабриката каждого вида на единицу продукции, общий объем полуфабрикатов и прибыль от единицы каждой продукции представлены в таблице:

полуфабрикаты	П1	П2	Объем полуфабрикат
I
II
прибыль

Нужно найти оптимальный план max прибыли.

Max Z =10 x₁ +35 x₂

X₁ + 2x₂ <=800

6 x₁ +2 x₂ <=2400

X₁ =>0

X₂ =>0

2 x₁ => x₂

Решение:

X₁ +2 x₂ =800

6 x₁ +2 x₂ =2400

X₁ =0

X₂ =0

2 x₁ = x₂

Множество планов, удовлетворяющих в системе ограничений задач линейного программирования, представляет собой пересечение конечного числа полупространства и поэтому является выпуклой.

Теорема: множество планов задач линейного программирования выпукло.

Графическим методом можно решить задачу линейного программирования с количеством n - переменных больше двух, если в ее канонической записи число неизвестных n и число линейно независимых уравнений m связаны соотношением n - m <=2, в этом случае каноническую форму задачи преобразуем в симметричную,которая будет содержать не более 2 переменных. Решаем задачу графически, находим 2 компонента оптимального плана, подставляя их в ограничение задачи, определяем остальные компоненты.

Пример: Двум погрузчикам разной мощности за 24часа нужно погрузить на первой площадке=230 тонн, на второй=168тонн. Первый погрузчик на первой площадке может погрузить 10тонн в час, на второй 12тонн в час. Второй погрузчик на каждой площадке по 13 тонн в час. Стоимость работ, связанных с погрузкой 1тонна первым погрузчиком на первой площадке 8 условных единиц. На второй площадке 7 условных единиц. Вторым погрузчиком на первой площадке 12 условных единиц, на второй площадке 13 условных единиц.

Решение: Необходимо составить план работы, т.е. найти какой объем работ должен выполнять каждый погрузчик на каждой площадке, чтобы стоимость всех работ по погрузке была минимальной. Причем по техническим причинам первый погрузчик на второй площадке должен работать не более 16 часов.

	П1	П2	t
Iпогрузчик
IIпогрузчик
задание

Min Z =8 x₁₁ +7 x₁₂ +12 x₂₁ +13 x₂₂

X₁₁ + x₂₁ =230

X₁₂ + x₂₂ =168

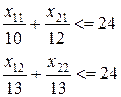
X₁₁ X₁₂ x₂₁ x₂₂ >0

X₂₁ =230 – x₁₁

X₂₂ =168 - x₁₂

Min Z =8 x₁₁ +7 x₁₂ +12(230 – x₁₁)+13(168 - x₁₂)= 8 x₁₁ +7 x₁₂ +2760-12 x₁₁ +2184-13 x₁₂ =4944- x₁₁ -6 x₁₂

6 x₁₁ +5 x₁₂ <=1440

X₁₁ + x₁₂ =>86

398- x₁₁ - x₁₂ <=312

- x ₁₁ - x₁₂ <=86

X₁₁ + x₁₂ =>86

X₁₁ <=230

X₁₂ <=168

Min Z =4944-(9 x₁₁ +6 x₂₁)

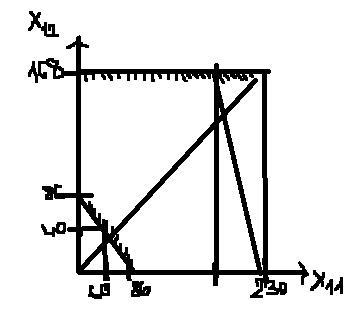
6 x₁₁ +5 x₁₂ =1440

X₁₁= 240-

X₁₂ =86- x₁₁

X₁₁ =100

X₁₂ =168

X₂₁ =130

X₂₂ =0

Min Z =400+1008=1408

X₁₁ =4944-1408=3536

Дата добавления: 2014-01-07