Связь между потенциальной энергией и силой

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы 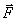, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии 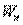. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

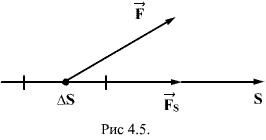
Для установления этой связи вычислим элементарную работу 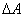, совершаемую силами поля при малом перемещении 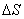тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой . Эта работа равна

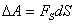
где 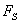- проекция силы 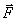на направление .

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии 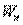, она равна убыли потенциальной энергии 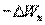на отрезке оси :

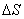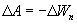
Из двух последних выражений получаем

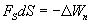
Откуда

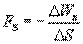
Последнее выражение дает среднее значение 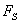на отрезке 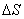. Чтобы

получить значение 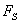в точке нужно произвести предельный переход:

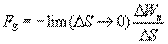
Так как 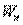может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от 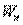по :

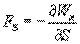
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

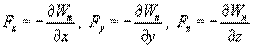
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

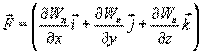
в математике вектор ,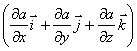

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом 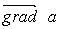. Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком

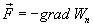
(4.15)

5. Динамика вращательного движения твердого тела. Введение

В динамике поступательного движения материальной точки были введены в дополнение к кинематическим величинам, понятия силы и массы. Аналогично, для изучения динамики вращательного движения тела, помимо рассмотренных кинематических характеристик, вводятся новые величины - момент силы, момент инерции и момент импульса.

5.1. Особенности вращательного движения

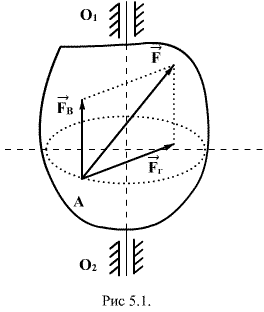
Рассмотрим движение твердого тела, имеющею ось вращения 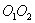под действием произвольно направленной силы 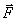, приложенной к телу в некоторой точке А, которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить.Горизонтальная составляющая , если она не пересекается с осью 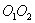вызывает вращение тела. Действие этой силы зависит от ее числового значения и расстояния линии действия от оси вращения.

5.2. Вращающий момент (или момент силы)

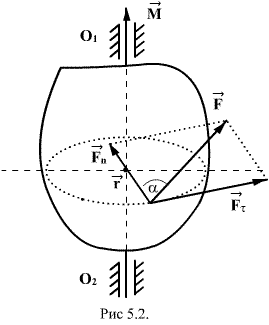
Сила 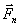пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей 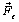тело будет совершать вращательное движение вокруг оси 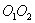. Расстояние 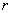от оси вращения до линии вдоль которой действует сила 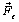называется плечом силы 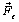. Моментом силы относительно точки О называется произведение модуля силы 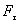на плечо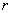

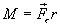
С учетом, что

момент силы

.

С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора 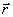, проведенного в точку приложения силы 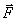на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен

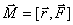
(5.1)

Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы 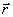и 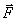, и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от 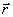к 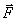происходит против часовой стрелки).

5.3. Момент инерции материальной точки относительно неподвижной оси вращения

Согласно второму закону Ньютона, для тангенциальной составляющейсилы 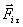, действующей на материальную точку массой m, и ускорения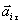

можем записать

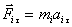
С учетом, что

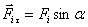и

имеем

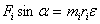
Домножимлевую и правую части на 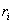и получим

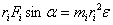
(5.2)

или

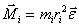
Произведение массы материальной точки 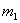тела на квадрат ее расстояния 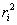до оси вращения называется моментом инерции материальной точки относительно оси вращения:

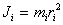
(5.3

5.4. Момент инерции твердого тела

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело

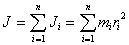
(5.4)

В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами 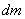, и моменты инерции тела определяется интегралом

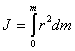
(5.5)

о где 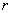- расстояние от элемента 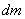до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью
плотности

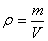
(5.5)

где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.

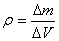
Плотность в данной точке в этом случае определяется следующим образом

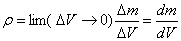
и тогда

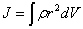
(5.6)

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

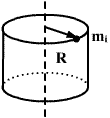
Момент инерции полого цилиндра с тонкими стенками, радиуса R.

Для полого цилиндра с тонкими стенками

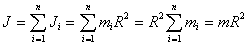
Сплошной однородный диск. Ось вращения является осью диска радиуса 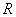. и массы m с плотностью 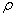Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки 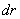и массой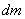. Для него

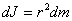
Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:

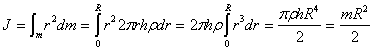
Момент инерции шара относительно оси, проходящей через центр тяжести.

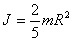
Момент инерции стержня длиной L и массой m относительно оси, проходящей:

а) через центр стержня -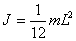

б) через начало стержня -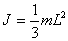

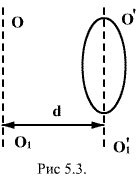
Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс 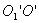известен. Необходимо определить момент инерции относительно произвольно оси 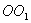параллельной оси 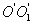. Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:

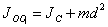
(5.7)

5.5. Второй закон Ньютона для вращательного движения и его анализ

С учетом (5.2) и (5.3) вращающий момент тела

(5.8)

или

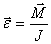
Это выражение представляет собой аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение 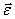твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела.

Дата добавления: 2014-01-07