Закон Ома. Закон Джоуля-Ленца

Классическая теория электропроводности

Почти сто лет тому назад П.Друде разработал теорию электро- и теплопроводности металлов. В теории Друде валентные электроны металла рассматривались как классический "электронный" газ (идеальный газ из электронов). Применение к этой модели основных положений элементарной молекулярно-кинетической теории привело к поразительным результатам. На основе этих представлений оказалось возможным объяснить закон Видемана-Франца, объяснить эффект Холла, возникновение контактной разности потенциалов, явление термоэлектронной эмиссии. Для всех перечисленных явлений удалось получить количественные зависимости между величинами, определяющими то или иное явление. Теория Друде не свободна от внутренних противоречий. Современная физика твердого тела базируется на представлениях квантовой механики, а для описания свойств электронного газа используется квантовая статистика, отличная от статистики Максвелла - Больцмана. Вместе с тем теория Друде не потеряла своей полезности: отдельные ее результаты поражают своей точностью, а методы теории Друде на редкость физически наглядны.

В рамках элементарной кинетической теории полагаем, что валентные электроны (электроны проводимости) металлов представляют собой одинаковые твердые сферы, двигаются они по прямым линиям до столкновения друг с другом, время контакта частиц пренебрежимо мало по сравнению с временем "свободного" движения.

Объемную концентрацию электронов проводимости можно оценить выражением:

(6.30)

где - объемная плотность металла (кг/м³), Z - валентность химического элемента, N_a - число Авогадро, А - относительная атомная масса элемента.

Заряд электрона е =-1,6*10^-19 Кл, масса электрона m_e = 0,91*10^-30 кг. Величину "е" ниже будем считать положительной, а знак заряда электрона будем учитывать непосредственно в формулах.

Плотность электронного газа:

(6.31)

значительно больше плотности обычных газов при нормальных условиях.

В теории Друде пренебрегают сильным электрон-электронным и электрон-ионным взаимодействием, полагая, что внутри металлического тела отдельный электрон практически ведет себя как свободная частица. Это дает нам право считать электрон "нейтральной" частицей при расчете взаимодействия ее с остальными частицами, но способной переносить заряд при расчете параметров электрического тока.

Рис. 6.1.

П.Друде полагал, что электроны в своем движении сталкиваются с атомами (ионами) кристаллической структуры металла (столкновения электрон-электрон значительно менее вероятны). Картина последовательных соударений электрона с атомами кристаллической решетки показана на рис. 6.1.

Современная теория оценивает вероятность такого механизма не очень высоко: рассеяние электронов имеет и другие механизмы. Поэтому не следует наглядную картину рис.6.1 понимать в буквальном смысле.

Будем считать, что отношение

(6.32)

представляет собой вероятность соударения электрона с рассеивающим центром, где dt - промежуток времени, - время релаксации или время свободного пробега. Предполагается, что величина 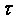не зависит от пространственного положения электрона и не меняется от соударения к соударению. Предполагается также, что электроны находятся в состоянии теплового равновесия со своим окружением. Механизм соударения детализируется следующим образом: скорость электрона после соударения статистически не связана со скоростью электрона до соударения (электрон "забыл" свою предысторию), направление скорости после соударения - случайное, хаотическое, а ее величина соответствует той температуре, которая имеет место в окрестности точки соударения.

Итак, рассмотрим закон Ома для однородного участка цепи в дифференциальной форме:

(6.33)

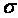- электропроводность, 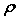- удельное электрическое сопротивление среды, - объемная плотность тока, - напряженность электрического поля. Вспомним, что величина - плотность потока электрического заряда

(6.34)

где 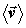- вектор средней скорости направленного движения носителей заряда, в рассматриваемом случае - электронов. В отсутствие напряженности электрического поля величина обращается в нуль (хотя хаотическое тепловое движение электронов продолжает иметь место). Для случая величина и направлена противоположно полю. Эту скорость можно рассчитать следующим образом. Пусть t - время, прошедшее с момента последнего соударения электрона с рассеивающим центром. Мгновенная скорость электрона в момент времени t равна:

(6.35)

Из-за "хаотичности" начальной скорости ее вклад в среднюю скорость частицы равен нулю, поэтому можно записать:

(6.36)

поскольку среднее время движения электрона между соударениями равно . В этом случае получим:

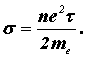
(6.37)

Заметим, что по Ланжевену из соотношения (6.36) следует выражение для "подвижности" электронов проводимости в металле:

(6.38)

Если по экспериментальным данным для 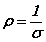оценить величину , она оказывается величиной порядка 10^-14 - 10^-15 с. Оценить длину свободного пробега можно соотношением

(6.39)

а значение можно получить из классического закона распределения энергии по степеням свободы

(6.40)

где k - постоянная Больцмана, Т - абсолютная температура металла. Из зависимости (6.40) при комнатной температуре получаем , а .

Значение величины l удивительно совпало с возможными значениями межатомных расстояний... Вроде бы теория Друде "правильно" описала механизм рассеяния электронов... На самом деле картина рассеяния имеет более сложную природу. И эксперимент не свидетельствует в пользу теории Друде: при достаточно низких температурах на тщательно приготовленных образцах можно получить , т.е. 10⁸ межатомных расстояний.

Итак, если бы мы знали , то зависимость (6.37) решала бы проблему расчета величины 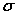. Более того, результаты теории Друде, не содержащие время релаксации , оказываются количественно верными.

Теория Друде объясняет физическую природу закона Джоуля-Ленца следующим образом. При каждом "соударении" с рассеивающим центром электрон передает этому центру энергию

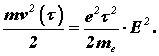
За единицу времени происходит таких соударений. А если учесть, что в единице объема содержится n электронов, то получим, в единице объема кристаллической решетки металла за единицу времени выделяется энергия, равная

Полученное соотношение обосновывает дифференциальную форму закона Джоуля-Ленца.

Дата добавления: 2014-01-07