Формула Ньютона-Лейбница

Предположим, что функция непрерывна на отрезке 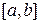. Будем рассматривать интегралы от этой функции на отрезках при всевозможных 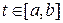. Очевидно, что результат интегрирования зависит от значения верхнего предела интегрирования. Поэтому обозначим . Имеем .

Рассмотрим 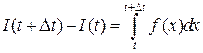. В соответствии с теоремой о среднем существует такое значение , что 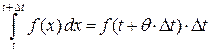. Следовательно, 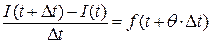. Переходя в последнем равенстве к пределу при 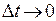и пользуясь непрерывностью функции в точке 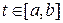, получим

.

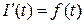Последнее означает, что функция 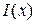является первообразной для функции . Следовательно, если 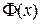– любая первообразная функции , то 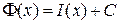по свойству двух первообразных одной и той же функции. Следовательно, 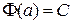, так как 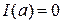, и . Значит,

.

Последняя формула, называемая формулой Ньютона-Лейбница, как раз обеспечивает связь между интегралом Римана (его еще называют определенным интегралом) и первообразными. Формулу Ньютона-Лейбница еще записывают в виде

,

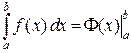где вертикальная черта и индексы обозначают разность значений функций, соответственно, при верхнем и нижнем значениях переменной.

Приложения интеграла Римана

Интеграл Римана по отрезку был нами введен как площадь криволинейной трапеции. Понятие площади неотделимо от понятия интеграла. С его помощью можно вычислять площади любых плоских областей, а также длины дуг, площади поверхностей и объемы тел.

1.Вычислить площадь области, расположенной между двумя кривым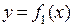и и и над отрезком , причем .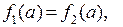

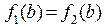Очевидно, что площадь области между кривыми равна разности площадей соответствующих криволинейных трапеций, поэтому

.

2. Вычислить площадь криволинейного сектора, ограниченного лучами (в полярных координатах) 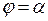и , а также заданной в полярных координатах кривой .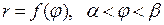

Проведем внутри криволинейного сектора лучи 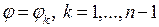, разбивающие исходный сектор на мелкие криволинейные секторы 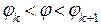, причем .

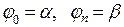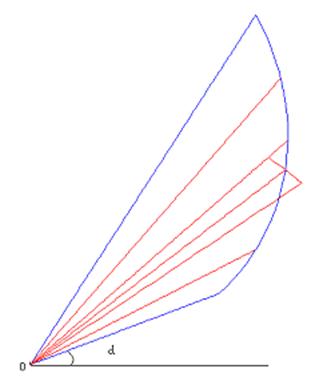
Заменим каждый мелкий криволинейный сектор круговым сектором с тем же углом при вершине и радиусом, равным значению , где . Тогда площадь кругового мелкого сектора равна 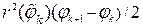. При этом чем меньше разность 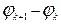, тем меньше площадь кругового мелкого сектора отличается от площади соответствующего криволинейного мелкого сектора.

При достаточно частом разбиении исходного криволинейного сектора площадь его достаточно близка к величине

.

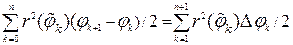Если теперь устремить к нулю наименьший из растворов малых криволинейных секторов, мы получим предел интегральных сумм – интеграл , который совпадает с площадью исходного криволинейного сектора.

3.Вычислить длину дуги кривой 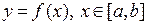. Длиной дуги кривой мы будем называть предельную сумму длин вписанных в дугу хорд при стремлении этих хорд к точкам.

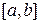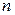Разобъем отрезок на отрезков 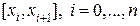, где . Длина хорды, расположенной над отрезком 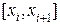, равна . Воспользуемся формулой конечных приращений Лагранжа и получим длину этой же хорды в ви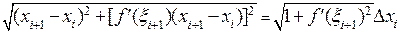де

, где ,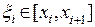

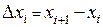. Таким образом, длина дуги всей кривой может быть приближена суммой 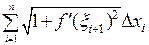, причем чем мельче разбиение отрезка 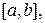тем точнее результат. При стремлении длины наименьшего из отрезков разбиения к нулю мы получим из суммы интеграл: 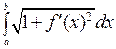, который и дает выражение длины дуги данной кривой.

4. Вычислить длину дуги пространственной кривой, заданной параметрически в виде

для вычисления ее длины применяют формулу

.

Дата добавления: 2014-01-07