Лекция 4. Тема «Напряжения и деформации в пластической области деформирования твердого тела»

Тема «Напряжения и деформации в пластической области деформирования твердого тела»

Для пластических тел Закон Гука соблюдается лишь в области малых деформаций. Дальнейшее деформирование приводит:

• хрупкому разрушению тел;
• к появлению пластических (необратимых) деформаций;
• к потере пропорциональности между напряжениями и деформациями.

В зависимости от вида функции напряжения от деформации различают хрупкие – 1, упрочняющиеся – 2 и идеально упругопластические – 3 тела (рис 1.)

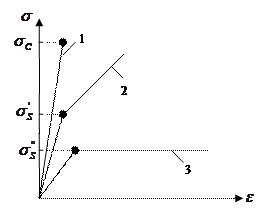Из рисунка видно, что хрупкие тела деформируется упруго вплоть до разрушения. При неизменном напряже-нии называемой

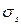-предела текучести.

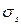- предел прочности крупного тела.

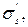
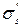- предел текучести

Упрочняющая тела характерезуются изменением вида зависимости напряжения от деформации при увеличениии напряжения больше, чем предел текучести материала, однако для увеличения деформации напряжения (нагрузку) необъходимо увеличывать. Область деформирования, в которой напряжение превышает предел текучести, называю пластической.

В общем случае уравнения (уравнения Генки), связывающие деформации и напряжения в пластичных телах, имеют вид:

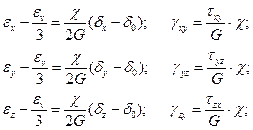
где 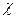-модуль пластичности, 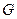- модуль деформации при сдвиге в упругой области.

В большинстве задач механики горных пород величиной 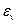можно пренебречь (условие не сжимаемости). В этом случае условие

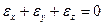
позволяет решать некоторые задачи, не прибегая к уравнениям Генки.

Рассмотрим условия перехода твердых тел из упругого состояния в пластическое, сформулированные исходя из опытных данных.

Условие Треска–Сен–Венана. Французский инженер Треск высказал предположение, что состояние пластичности наступает тогда6 когда во всех точках среды максимальное касательное напряжение достигает определенного значения. Позднее Сен –Венан математический описал это условие

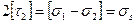
где 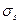- предел текучести материала при простом растяжении.

Из этого выражения следует, что главное промежуточное напряжения 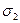не влияет на состояние текучести, что не всегда подтверждается опытом.

Условие Мизеса. В соответствии с условием Мизеса состояние пластичности наступает тогда, когда удельная упругая энергия формоизменения достигнет определенной величины, характерной для материала данного тела.

Упругая удельная энергия деформирования

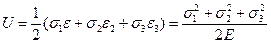
Представим величину 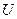как сумму энергии упругого изменения объема 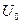и упругого изменения формы .

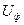Удельная упругая энергия изменения объема

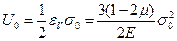
тогда удельная упругая энергия изменения формы

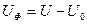
После постановки в это выражения значения составляющих (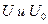), а также соответствующие и преобразование, нормам

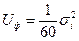
Из этого выражения следует, что момент достижения предельного состояния при переходе от упругого состояния твердого тела и пластическому однозначно определяется интенсивностью главных напряжении.

Дата добавления: 2014-01-07