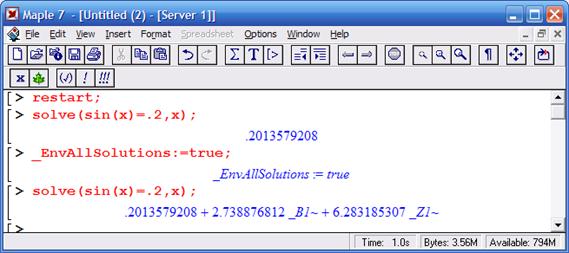
Решение тригонометрических уравнений

Решение неравенств

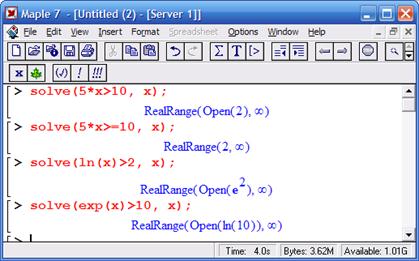
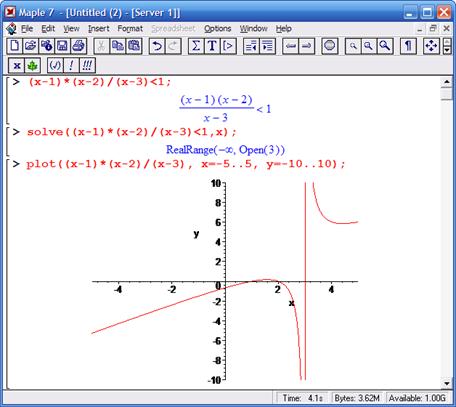
Неравенства в математике встречаются почти столь же часто, как и равенства. Они вводятся знаками отношений, например: > (больше), < (меньше) и т. д. Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные на рис. 8.15 примеры поясняют технику решения неравенств.

Из приведенных примеров очевидна форма решений – представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумным является построение графика выражения, которое задает неравенство, – это позволяет наглядно убедиться в правильности решения. Приведем еще несколько примеров решения неравенств в аналитической форме:

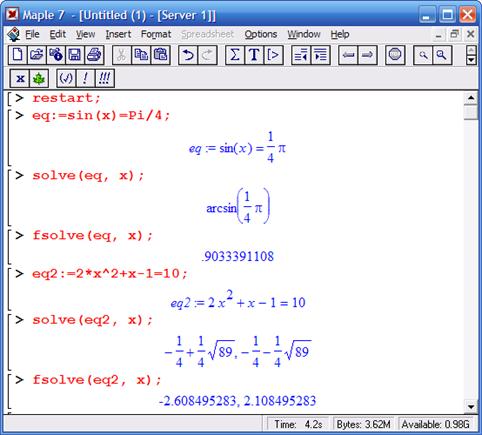
Решение в численном виде – функция fsolve

Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в форме вещественных чисел удобно использовать функцию fsolve

fsolve(eqns, vars);

Решение дифференциальных уравнений.

Дифференциальные уравнения лежат в основе математического моделирования различных, в том числе физических, систем и устройств. Это анализ поведения различных систем во времени (анализ динамики) – полет тела, брошенного под углом к горизонту; вычисление различных полей (тяготения, электрических зарядов).

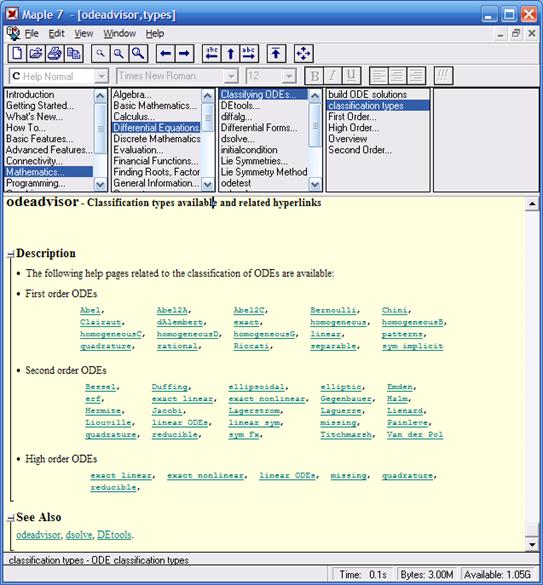
На следующем слайде представлен раздел справки Maple с классификацией дифференциальных уравнений. В ней представлено:

· 20 дифференциальных уравнений первого порядка;

· 25 дифференциальных уравнений второго порядка;

· 6 типов дифференциальных уравнений высшего порядка

· а также основные функции решения дифференциальных уравнений

Maple позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде.

Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи:

dsolve(ODE);

dsolve(ODE, переменная);

dsolve({ODE, нач_услович}, переменная);

Примеры решения дифференциальных уравнений.

Начнем рассмотрение практических примеров с решения простых одинарных обыкновенных дифференциальных уравнения (ОДУ) первого порядка в символьном виде.

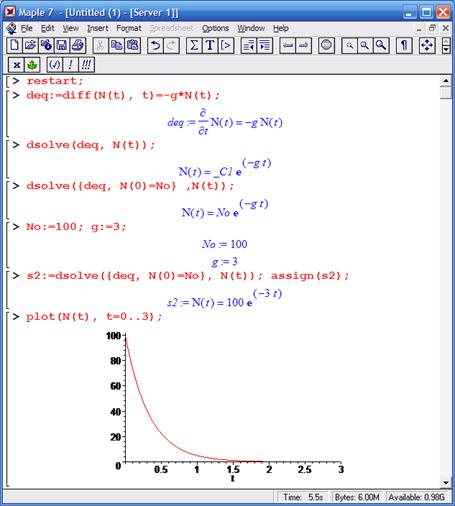
Запишем дифференциальное уравнение радиоактивного распада атомов:

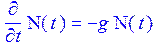
В математическом пакете эта запись имеет вид:

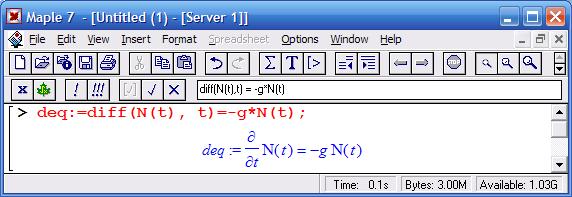
Используя функцию dsolve, получим его общее аналитическое решение:

В решении присутствует произвольная постоянная _С1. Но ее можно заменить на постоянную N(0)=N₀, означающую начальное число атомов в момент времени t=0

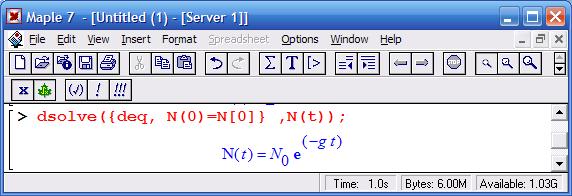
Далее можно ввести начальные условия. Например, в начальный момент времени у нас было 100 атомов, а постоянная распада равна 3:

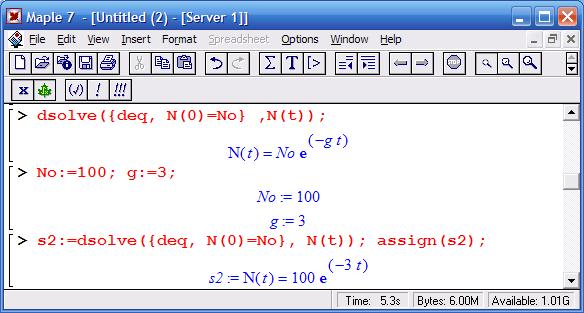
Теперь мы можем воспользоваться полученной зависимостью N(t) и построить график:

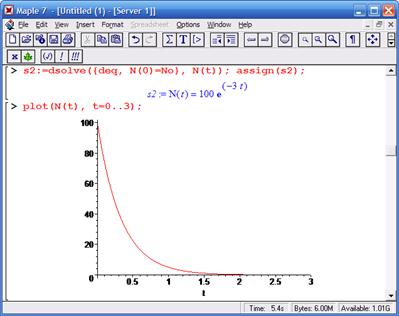
график описывает экспоненциальный закон уменьшения числа атомов вещества в ходе его радиоактивного распада.

Другие примеры решения ОДУ первого порядка

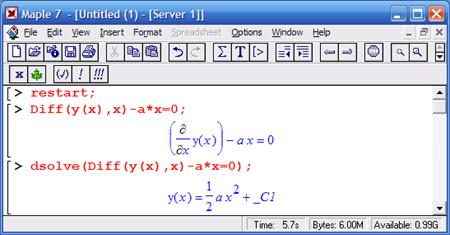
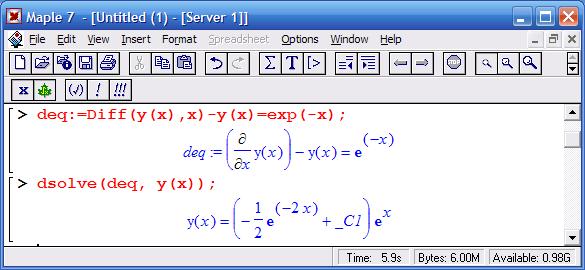
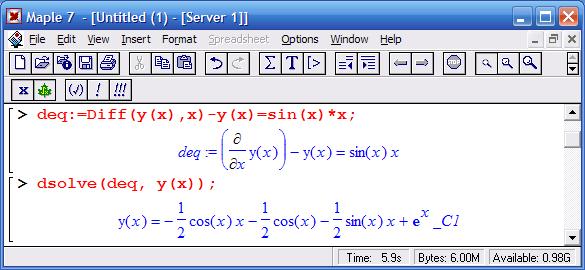
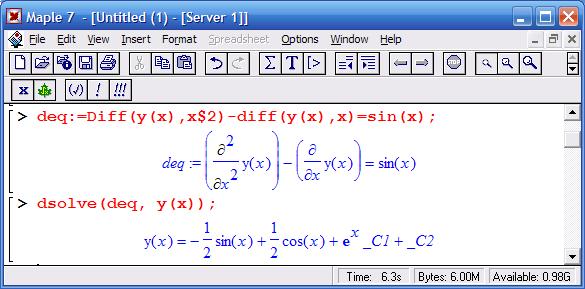
Из приведенного выше примера видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ в ней можно задать производную более высокого порядка.

Рассмотрим физический пример: полет тела, брошенного вверх

Многие физические явления, связанные с движением объектов, в соответствии со вторым законом Ньютона, описываются дифференциальным уравнением второго порядка.

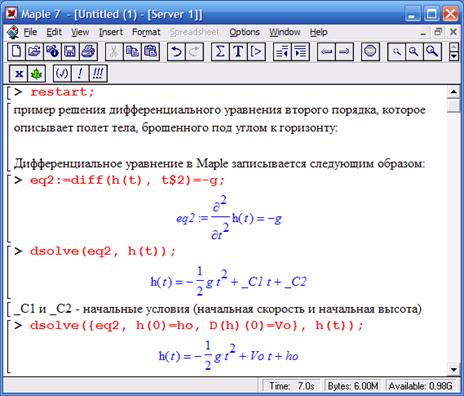
На данном этапе получено общее уравнение для временной зависимости высоты тела h(t). Далее можно подставить конкретные данные и получить график зависимости полета тела от времени.

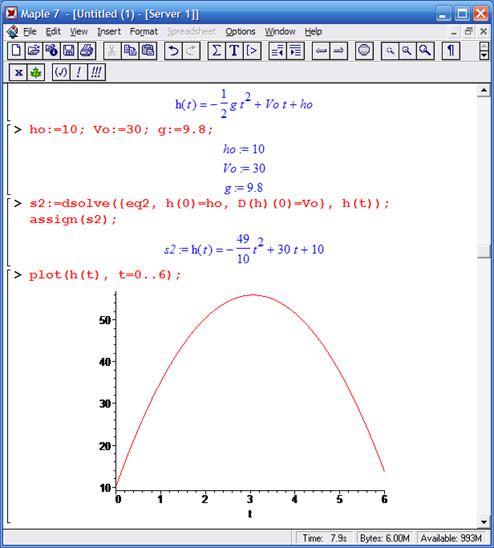
Дата добавления: 2014-01-07