Формульная постановка задачи

Наряду со словесной возможна математическая (формульная) постановка задачи.

Математическая постановка представляет собой конкретные зависимости вычисления искомых функций с указанием исходных данных.

Математическая формулировка может быть выполнена для всей задачи в целом или являться частью словесной.

В первом случае задача, как правило, чисто абстрактная. Входные данные могут задаваться отдельно или численными значениями в расчётных зависимостях. При этом они не имеют физической сути и, естественно, размерностей.

Рассмотрим две задачи с математической формулировкой.

Пример 1.4. Рассчитать значение функции

,

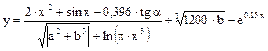если a=12; b= -9,2; x=2,75; 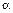=0,76.

Пример 1.5. Рассчитать корни квадратного уравнения 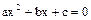по стандартной зависимости

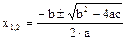, если a=1,4; b=11,2; c= -7,8.

В примере 2.4 формулировка практически полностью представлена одной математической зависимостью, в примере 2.5 – математическая формулировка является частью словесной.

Типичными примерами частично математически сформулированных, являются задачи расчета площадей (объемов) геометрических фигур.

Пример 1.6. Рассчитать площади круга (в см²) по известной зависимости 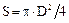, если диаметр изменяется от 35 см до 120 см с шагом 15 см.

Каждая из законченных постановок задач позволяет перейти к следующему этапу – созданию программного продукта.

Дата добавления: 2014-01-07