
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разложение функций в степенные ряды
|
|
|
|
1.1. Ряды Тейлора и Маклорена
Для приложений важно уметь данную функцию  разлагать в степенной ряд, т. е. функцию
разлагать в степенной ряд, т. е. функцию  представлять в виде суммы степенного ряда.
представлять в виде суммы степенного ряда.
Как известно, для любой функции  , определенной в окрестности точки
, определенной в окрестности точки 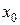 и имеющей в ней производные до
и имеющей в ней производные до 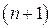 -го порядка включительно, справедлива формула Тейлора:
-го порядка включительно, справедлива формула Тейлора:
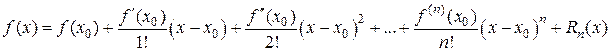 , (1.1)
, (1.1)
где 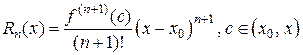 , – остаточный член в форме Лагранжа. Число с можно записать в виде
, – остаточный член в форме Лагранжа. Число с можно записать в виде 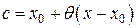 , где
, где  . Формулу (1.1) можно кратко записать в виде
. Формулу (1.1) можно кратко записать в виде

где  – многочлен Тейлора.
– многочлен Тейлора.
Если функция  имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки х0, и остаточный член
имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки х0, и остаточный член 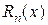 стремится к нулю при
стремится к нулю при 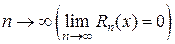 , то из формулы Тейлора получается разложение функции
, то из формулы Тейлора получается разложение функции  по степеням
по степеням 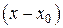 , называемое рядом Тейлора:
, называемое рядом Тейлора:
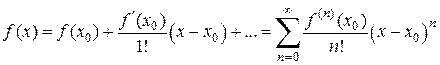 (1.2)
(1.2)
Если в ряде Тейлора положить 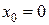 , то получим разложение функции по степеням х в так называемый ряд Маклорена:
, то получим разложение функции по степеням х в так называемый ряд Маклорена:
 (1.3)
(1.3)
Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки  . Но отсюда ещё не следует, что он будет сходиться к данной функции
. Но отсюда ещё не следует, что он будет сходиться к данной функции  ; он может оказаться расходящимся или сходиться, но не к функции
; он может оказаться расходящимся или сходиться, но не к функции  . Так, например, функция
. Так, например, функция
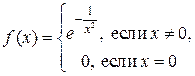
имеет в точке 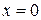 производные всех порядков, причем
производные всех порядков, причем 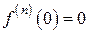 при всяком n.
при всяком n.
Ряд Маклорена имеет вид
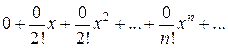 .
.
Он сходится, но его сумма 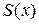 в любой точке х равна нулю, а не
в любой точке х равна нулю, а не  .
.
Пусть для функции  составлен соответствующий ей ряд Тейлора.
составлен соответствующий ей ряд Тейлора.
Теорема 1. Для того, чтобы ряд Тейлора (1.2) функции  сходился к
сходился к  в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (1.1) стремился к нулю при
в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (1.1) стремился к нулю при 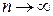 , т. е. чтобы
, т. е. чтобы 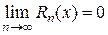 .
.
Пусть ряд Тейлора (1.2) сходится к функции  в некоторой окрестности точки
в некоторой окрестности точки 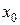 , т. е.
, т. е. 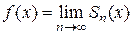 . Так как n- я частичная сумма
. Так как n- я частичная сумма 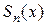 ряда (1.2) совпадает с многочленом Тейлора
ряда (1.2) совпадает с многочленом Тейлора 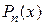 , т. е.
, т. е. 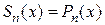 , находим
, находим
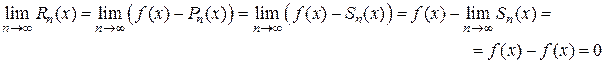
Обратно, 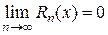 . Тогда
. Тогда
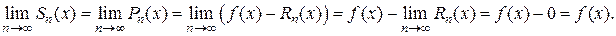
Замечание. Если ряд Тейлора (1.2) сходится к порождающей функции  , то остаточный член формулы Тейлора равен остатку ряда Тейлора, т. е.
, то остаточный член формулы Тейлора равен остатку ряда Тейлора, т. е. 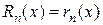 . (Напомним, что
. (Напомним, что 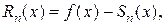 а
а 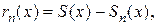 где
где 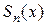 – сумма ряда Тейлора).
– сумма ряда Тейлора).
Таким образом, задача разложения функции  в степенной ряд сведена по существу к определению значений х, при которых
в степенной ряд сведена по существу к определению значений х, при которых 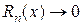 (при
(при 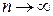 ). Если сделать это не просто, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции.
). Если сделать это не просто, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции.
На практике часто пользуются следующей теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.
Теорема 2. Если модули всех производных функций  ограничены в окрестности точки
ограничены в окрестности точки 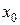 одним и тем же числом
одним и тем же числом 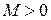 , то для любого х из этой окрестности ряд Тейлора функции
, то для любого х из этой окрестности ряд Тейлора функции  сходится к функции
сходится к функции  , т. е. имеет место разложение (1.2).
, т. е. имеет место разложение (1.2).
Согласно теореме 1, достаточно показать, что 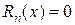 . По условию теоремы 2 для любого n имеет место неравенство
. По условию теоремы 2 для любого n имеет место неравенство 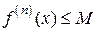 . Тогда имеем
. Тогда имеем
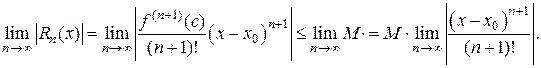
Осталось показать, что 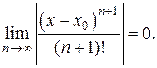 Для этого рассмотрим ряд
Для этого рассмотрим ряд
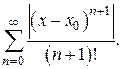
Так как
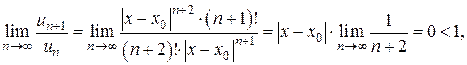
то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда в силу необходимого признака сходимости,
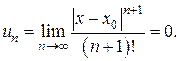
Следовательно, 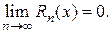
1.2. Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)
Для разложения функции  в ряд Маклорена (1.3) нужно:
в ряд Маклорена (1.3) нужно:
а) найти производные 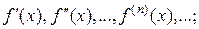
б) вычислить значения производных в точке 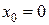 ;
;
в) написать ряд (1.3) для заданной функции и найти его интервал сходимости;
г) найти интервал 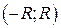 , в котором остаточный член ряда Маклорена
, в котором остаточный член ряда Маклорена 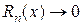 при
при 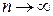 . Если такой интервал существует, то в нем функция
. Если такой интервал существует, то в нем функция  и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.
Замечание. В интервале сходимости степенного ряда остаточный член стремится к нулю при 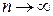 .
.
Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить):
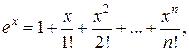
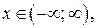 (1.4)
(1.4)
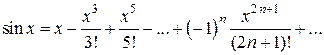
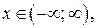 (1.5)
(1.5)
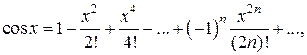
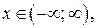 (1.6)
(1.6)
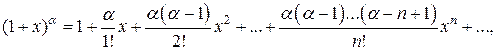
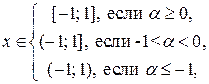 (1.7)
(1.7)
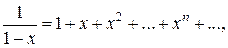
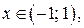 (1.8)
(1.8)
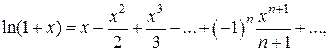
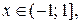 (1.9)
(1.9)

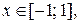 (1.10)
(1.10)
 (1.11)
(1.11)

 (1.12)
(1.12)
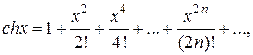
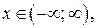 (1.13)
(1.13)
Докажем формулу (1.4). Пусть 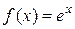 .
.
Имеем:

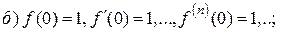

т. е. ряд сходится в интервале  ;
;
г) для всех  имеем
имеем 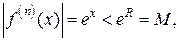 т. е. все производные в этом интервале ограничены одним и тем же числом
т. е. все производные в этом интервале ограничены одним и тем же числом 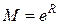 . Следовательно, по теореме 2
. Следовательно, по теореме 2 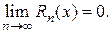 Таким образом,
Таким образом, 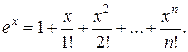
Докажем формулу (1.5). Пусть 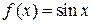 .
.
Имеем:
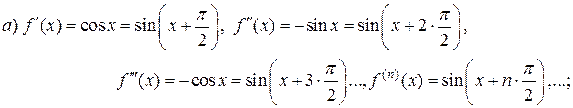
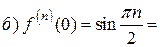
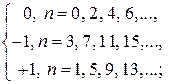
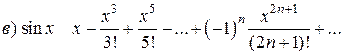 Легко проверить, что полученный ряд сходится на всей числовой оси, т. е. при всех
Легко проверить, что полученный ряд сходится на всей числовой оси, т. е. при всех 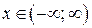 ;
;
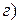 любая производная функции
любая производная функции 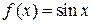 по модулю не превосходит единицы,
по модулю не превосходит единицы,
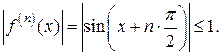
Следовательно, по теореме 2 имеет место разложение (1.5).
Пример 1. Разложить в ряд Маклорена функцию 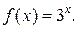
Решение. Так как 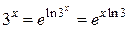 , то заменяя х на
, то заменяя х на 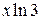 в разложении (1.4), получим
в разложении (1.4), получим
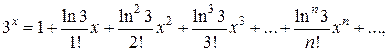
 .
.
Пример 2. Выписать ряд Маклорена функции 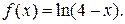
Решение. Так как
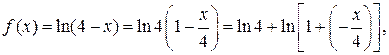
то, воспользовавшись формулой (1.9), в которой заменим х на 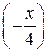 , получим:
, получим:
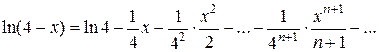 ,
,
если 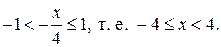
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1049; Нарушение авторских прав?; Мы поможем в написании вашей работы!