Достаточные признаки разложимости в ряд Фурье.

Некоторые приложения степенных рядов

2.1 Приближенное вычисление значений функций

Пусть требуется вычислить значение функции при с заданной точностью .

Если функцию в интервале 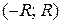можно разложить в степенной ряд

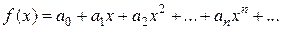
и 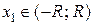, то точное значение 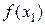равно сумме этого ряда при , т. е.

,

а приближенное – частичной сумме 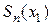, т. е.

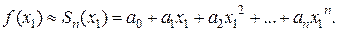
Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т. е.

,

где

.

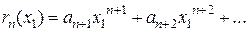Таким образом, ошибку можно найти, оценив остаток ряда.

Для рядов лейбницевского типа

В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки берут величину остатка этого нового ряда.

Пример 3. Найти 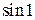с точностью до 0,001.

Решение. Согласно формуле (5),

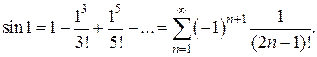
Стоящий справа ряд сходится абсолютно (проверить самостоятельно). Так как 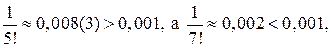то для нахождения 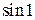с точностью до 0,001 достаточно первых трех слагаемых:

Допускаемая при этом ошибка меньше, чем первый отброшенный член(т. е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение 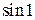примерно равно 0,84147.

Пример 4. Вычислить число у с точностью до 0,001.

Решение. Подставляя в формулу (4), получим

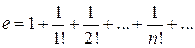
Справа стоит знакоположительный ряд. Возьмем n слагаемых и оценим ошибку :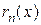

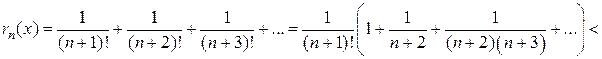
т. е. 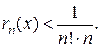Остается подобрать наименьшее натуральное число n, чтобы выполнялось неравенство 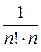< 0,001.

Нетрудно вычислить, ч то это неравенство выполняется при Поэтому имеем:

Замечание. Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена

,

где с находится между 0 и х₁. В последнем примере 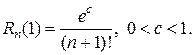Так как 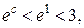то При n = 6 имеем: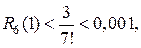

2.2. Приближенное вычисление определенных интегралов

Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции, либо нахождение первообразной сложно.

Пусть требуется вычислить 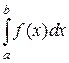с точностью до . Если подынтегральную функцию можно разложить в ряд по степеням x и интервал сходимости 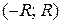включит в себя отрезок 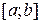, то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функции.

Пример 5. Вычислить интеграл с точностью до

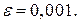
Решение. Разложим подынтегральную функцию в ряд Маклорена, заменяя х на в формуле (1.4):

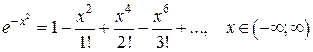(2.1)

Интегрируя обе части равенства (2.1) на отрезке , лежащем внутри интервала сходимости , получим:

=

=.

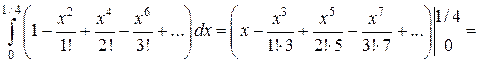
Получили ряд лейбницевского типа. Так как 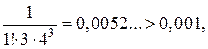а 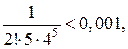то с точностью до 0,001 имеем:

Замечание. Первообразную для функции 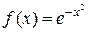легко найти в виде степенного ряда, проинтегрировав равенство (2.1) в пределах от 0 до х:

.

2.3. Приближенное решение дифференциальных уравнений

Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора.

Познакомимся с двумя способами решения дифференциальных уравнений с помощью степенных рядов.

Пусть, например, требуется решить уравнение

(2.2)

удовлетворяющее начальным условиям

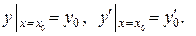(2.3)

а) способ последовательного дифференцирования

Решение уравнения (2.2) ищем в виде ряда Тейлора:

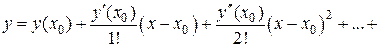
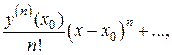(2.4)

при этом первые два коэффициента находим из начальных условий (2.3). Подставив в уравнение (2.2) значения находим третий коэффициент: . Значения находим путем последовательного дифференцирования уравнения (2.2) по х и вычисления производных при . Найденные значения производных (коэффициентов) подставляем в равенство (2.4). Ряд (2.4) представляет искомое частное решение уравнения (2.2) для тех значений х, при которых он сходится. Частичная сумма этого ряда будет приближенным решением дифференциального уравнения (2.2).

Рассмотренный способ применим и для построения общего решения уравнения (2.2), если и рассматривать как произвольные постоянные.

Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.

Пример 6. Методом последовательно дифференцирования найти первых пять членов (отличных от нуля) разложения в ряд решения уравнения .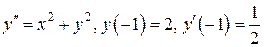

Решение. Будем искать решение уравнения в виде

Здесь 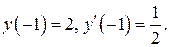Находим , подставив в исходное уравнение: 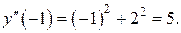Для нахождения последующим коэффициентов дифференцируем заданное дифференциальное уравнение:

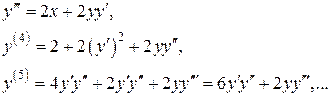
При имеем:

Подставляя найденные значения производных в искомый ряд, получим

.

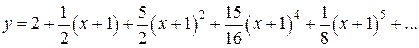б) способ неопределенных коэффициентов

Этот способ приближенного решения наиболее удобен для интегрирования линейных дифференциальных уравнений с переменными коэффициентами.

Пусть, например, требуется решить уравнение

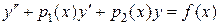(2.5)

с начальными условиями .

Предполагая, что коэффициенты и свободный член разлагаются в ряды по степеням 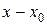, сходящиеся в некотором интервале 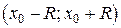, искомое решение 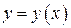ищем в виде степенного ряда

(2.6)

с неопределенными коэффициентами.

Коэффициенты и 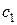определяются при помощи начальных условий

Для нахождения последующих коэффициентов дифференцируем ряд (2.6) два раза (каков порядок уравнения) и подставляем выражения для функции у и её производных в уравнение (2.5), заменив в нем , их разложениями. В результате получаем тождество, из которого методом неопределенных коэффициентов находим недостающие коэффициенты. Построенный ряд (2.6) сходится в том же интервале 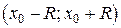и служит решением уравнения (2.5).

Пример 7. Найти решение уравнения

используя метод неопределенных коэффициентов.

Решение. Разложим коэффициенты уравнения в степенные ряды: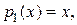

.

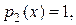
Ищем решение уравнения в виде ряда

.

Тогда

Из начальных условий находим: Подставляем полученные ряды в дифференциальное уравнение:

+.

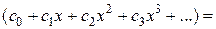
Приравниваем коэффициенты при одинаковых степенях х:

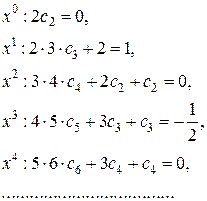
Отсюда находим, что Таким образом, получаем решение уравнения в виде

,

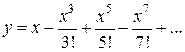т. е.

Теорема. (Теорема Дирихле) Если функция f(x) имеет период 2p и на отрезке [-p;p] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок [-p;p] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва его сумма равна , т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).

Функция f(x), для которой выполняются условия теоремы Дирихле называется кусочно – монотонной на отрезке [-p;p].

Теорема. Если функция f(x) имеет период 2p, кроме того, f(x) и ее производная f’(x) – непрерывные функции на отрезке [-p;p] или имеют конечное число точек разрыва первого рода на этом отрезке, то ряд Фурье функции f(x) сходится при всех значениях х, причем в точках непрерывности его сумма равна f(x), а в точках разрыва она равна . При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).

Функция, удовлетворяющая условиям этой теоремы, называется кусочно – гладкой на отрезке [-p;p].

Дата добавления: 2014-01-07