Дифференциальное уравнение изогнутой оси балки

Рассмотрим изгиб элементарного участка балки, заключенного между двумя бесконечно близкими поперечными сечениями балки, на расстоянии х от начала координат (рис. 18.2.1).

Рис. 18.2.1

ρ _x – радиус кривизны балки в сечении х определяется по формуле Бернулли (15.17):

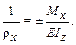
Из математики известно, что кривизна плоской кривой АВ (рис. 18.2.2) в произвольной точке Д определяется выражением (18.2.1):

(18.2.1)

Тогда для балки (рис. 18.2.1) имеем

,

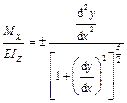где 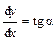– тангенс угла наклона касательной.

Однако в реальных конструкциях изогнутая ось балки представляет собой весьма пологую кривую, т. е. , тогда

,

т. е.

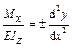, (18.2.2)

где M_x – изгибающий момент в сечении х (с учетом знака); E – модуль упругости I рода; I_z – момент инерции сечения относительно нейтральной линии.

Полученное дифференциальное уравнение изогнутой оси балки (18.2.2) является приближенным, т. к. при его выводе точное значение кривизны заменили приближенным, кроме того, не учитывали влияние поперечной силы. Однако, как показывает практика, это влияние является пренебрежимо малым.

Знак кривизны определяется знаком изгибающего момента (рис. 14.1.1, б).

Произведение EI_z, с увеличением которого уменьшаются величины углов поворота и прогибов, называется жесткостью балки при изгибе.

Дата добавления: 2014-01-07