
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Кастилиано
|
|
|
|
Кастилиано (1847–1844 гг.) – итальянский инженер. Окончил Туринский политехнический институт. Представленная им в 1873 г. научная работа на соискание звания инженера содержала формулировку знаменитой теоремы вместе с приложениями ее в теории сооружений.
Рассмотрим два состояния консольной балки (табл. 19.2.1).
Потенциальная энергия деформации балки в первом состоянии:
 .
.
Во втором состоянии:
 .
.
Однако из табл. 19.2.1 видно, что 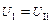 , т. е.
, т. е.
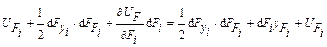 или
или
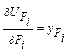 (19.2.1)
(19.2.1)
Таблица 19.2.1
I.

| II.
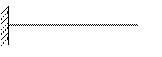
|
 Нагрузим балку системой сил: Нагрузим балку системой сил:
| Приложим к концу консоли элементарную силу d Fi:

|
В результате деформации прогиб точки приложения силы Fi равен 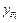 . Потенциальная энергия деформации равна . Потенциальная энергия деформации равна 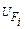 . Сообщаем силе Fi некоторое приращение d Fi: . Сообщаем силе Fi некоторое приращение d Fi:

| Потенциальная энергия деформации при этом равна 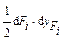 . Затем к деформированной балке приложим систему сил: . Затем к деформированной балке приложим систему сил:

|
Тогда сила d Fi совершит работу, равную 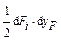 , а потенциальная энергия деформации получит приращение по силе dFi. , а потенциальная энергия деформации получит приращение по силе dFi.
| Тогда сила d Fi совершит работу, равную 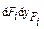 , а потенциальная энергия деформации от действия системы сил равна , а потенциальная энергия деформации от действия системы сил равна 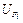 : : 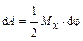 . .
|
Формула (19.2.1) называется теоремой Кастилиано: перемещение точки приложения силы равно частной производной от потенциальной энергии по этой силе.
Здесь сила F является обобщенной силой, т. е. под ней понимают любое силовое воздействие (сосредоточенная сила, пара сил и т. д.), а перемещение 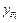 является обобщенным перемещением, соответствующим силе F.
является обобщенным перемещением, соответствующим силе F.
Например, если под обобщенной силой F понимают момент, то обобщенным перемещением будет угол поворота.
В общем случае теорему Кастилиано можно сформулировать так:
Частная производная от потенциальной энергии по обобщенной силе есть обобщенное перемещение точки приложения этой силы.
С помощью теоремы Кастилиано можно определить перемещения при различных видах деформаций, однако, существенным недостатком этой теоремы является то, что в сечении, где определяется перемещение, должна быть приложена соответствующая этому перемещению сила. Если же такой силы нет, то ее необходимо приложить, полагая равной нулю.
При наличии нескольких сил применение этой теоремы трудоемко.
 Пример 19.2.1. Определить прогиб сечения А (рис. 19.2.1), если EIz = const.
Пример 19.2.1. Определить прогиб сечения А (рис. 19.2.1), если EIz = const.
 Решение. Согласно теореме Кастилиано (19.2.1),
Решение. Согласно теореме Кастилиано (19.2.1), 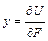 . В рассматриваемом сечении (т. А) действует сила F, соответствующая искомому перемещению – прогибу, т. е. теорема Кастилиано применима.
. В рассматриваемом сечении (т. А) действует сила F, соответствующая искомому перемещению – прогибу, т. е. теорема Кастилиано применима.
Определим потенциальную энергию деформации балки:
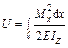 ,
,
где 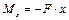 – изгибающий момент в произвольном сечении x (рис. 19.2.1), если
– изгибающий момент в произвольном сечении x (рис. 19.2.1), если 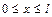 :
:
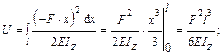
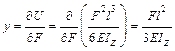 .
.
Знак «плюс» показывает, что направление прогиба y и силы F совпадают между собой (прогиб и сила направлены вниз).
Если бы перемещение получилось со знаком «минус», то это означало бы, что его направление противоположно направлению соответствующей силы.
Пример 19.2.2. Определить угол поворота сечения А (рис. 19.2.2), если EIz = const.
Решение. В рассматриваемом сечении нет силы, соответствующей искомому перемещению, поэтому необходимо в сечении А приложить сосредоточенный момент М = 0 (рис. 19.2.3), при этом направление момента соответствует предполагаемому направлению угла поворота сечения.

| 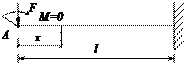
|
Рис. 19.2.2 Рис. 19.2.3
Согласно (19.2.1),
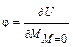 ;
; 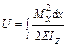 ,
,
где 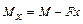 , если
, если 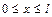 , тогда
, тогда
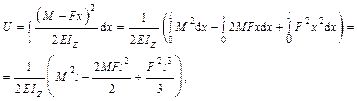
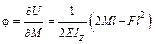 , но М = 0, тогда
, но М = 0, тогда
 .
.
Знак «минус» показывает, что угол поворота сечения А противоположен предполагаемому, т. е. направив момент М = 0 по часовой стрелке, мы предположим, что сечение А поворачивается по часовой стрелке, на самом деле сечение А поворачивается против часовой стрелки.
19.3. Теорема Максвелла – Мора
Рассмотрим теорему Кастилиано (19.2.1) для случая изгиба:
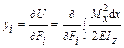 .
.
Применяя правило дифференцирования по параметрам, имеем
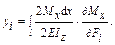 (19.3.1)
(19.3.1)
Английский ученый Максвелл (1831–1879 гг.) и немецкий ученый О. Мор (1835–1918 гг.) одновременно предложили заменить частную производную 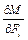 действием в искомом сечении обобщенной единичной силы (F). Тогда выражение (19.3.1) имеет вид:
действием в искомом сечении обобщенной единичной силы (F). Тогда выражение (19.3.1) имеет вид:
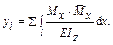 (19.3.2)
(19.3.2)
Полученную формулу (19.3.2) называют интегралом Мора, здесь yi – обобщенное перемещение (линейное, угловое); Mx – изгибающий момент в сечении х от заданной нагрузки;  – изгибающий момент в том же сечении от обобщенной единичной силы.
– изгибающий момент в том же сечении от обобщенной единичной силы.
Для его определения необходимо отбросить всю заданную нагрузку, а в сечение, где определяют перемещение, приложить безразмерную силу, равную единице, по направлению искомого перемещения (если определяют прогиб, то прикладывают вертикальную силу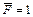 ; если угол поворота, то сосредоточенный момент
; если угол поворота, то сосредоточенный момент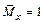 );
); 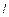 – длина участка.
– длина участка.
Порядок определения перемещений по теореме Максвелла – Мора (интегралом Мора):
1. Для каждого участка составить выражения изгибающих моментов от заданной нагрузки – Mx.
2. Мысленно отбросить всю заданную нагрузку и к сечению, перемещение которого требуется определить, приложить вертикальную безразмерную силы 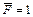 (при определении прогиба) или безразмерный единичный момент М = 1 при определении угла поворота.
(при определении прогиба) или безразмерный единичный момент М = 1 при определении угла поворота.
3. Для тех же участков (п. 1) составить выражения изгибающих моментов от единичной нагрузки 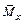 .
.
4. Вычислить интегралы из произведений 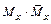 для каждого участка.
для каждого участка.
5. Результаты интегрирования сложить и разделить на жесткость EIz (если жесткость балки на каждом участке постоянная).
При этом положительное значение перемещения совпадает с направлением соответствующей единичной силы.
Пример 19.3.1. Определить прогиб сечения А (рис. 19.3.1), если EIz = const.
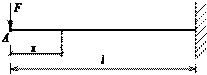
| 
|
a) б)
Рис. 19.3.1
Решение. Определим изгибающий момент в произвольном сечении балки (рис. 19.3.1, а)  , если
, если 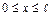 .
.
Отбросим заданную нагрузку, а в сечении А приложим вертикальную силу (т. е. определяем прогиб) 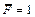 (рис. 19.3.1, б) и определим изгибающий момент
(рис. 19.3.1, б) и определим изгибающий момент 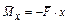 .
.
Подставив полученное выражение в интеграл Мора (19.3.1), получим:
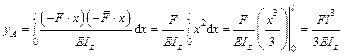 .
.
Знак «плюс» перемещения 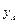 обозначает, что перемещение совпадает с выбранным направлением силы
обозначает, что перемещение совпадает с выбранным направлением силы 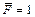 , т. е. направленно вниз.
, т. е. направленно вниз.
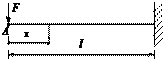 Пример 19.3.2. Определить угол поворота сечения А (рис. 19.3.2, а), если EIz= const.
Пример 19.3.2. Определить угол поворота сечения А (рис. 19.3.2, а), если EIz= const.
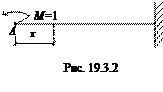 Решение. Изгибающий момент от заданной нагрузки (рис. 19.3.2, а)
Решение. Изгибающий момент от заданной нагрузки (рис. 19.3.2, а)  , где
, где 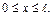
Отбросим заданную нагрузку, а в сечении А приложим сосредоточенный момент (т. к. определяем угол поворота):
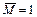 , тогда
, тогда 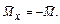
Подставив в (19.3.1), имеем
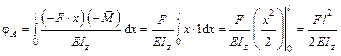 .
.
Знак «плюс» перемещения φ A означает, что сечение А поворачивается против часовой стрелки (по направлению 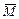 ).
).
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2590; Нарушение авторских прав?; Мы поможем в написании вашей работы!