Раскрытие статической неопределимости балок

Методика расчета балок методом сил

Раскрытие статической неопределимости методом сил производится в следующей последовательности:

1. Определяют степень статической неопределимости.

2. Отбрасывают «лишние» закрепления. При этом балка превращается в статически определимую, которая называется основной системой.

3. К основной системе прикладывают заданную нагрузку и реакции отброшенных связей, обозначая их x ₁, x ₂, …, x_n, полученная система называется эквивалентной системой.

4. Для основной системы составляют уравнения совместимости деформаций, которые имели «лишние» закрепления. Необходимое количество таких уравнений должно быть равно степени статической неопределимости балки.

5. Раскрывают статическую неопределимость балки, решая уравнения совместимости деформаций.

На этом заканчивается раскрытие статической неопределимости. Остальные реакции определяют из уравнений статики.

Если в результате раскрытия статической неопределимости реакции получаются со знаком «минус», то это означает, что их действительное направление противоположно направлению, принятому в основной системе.

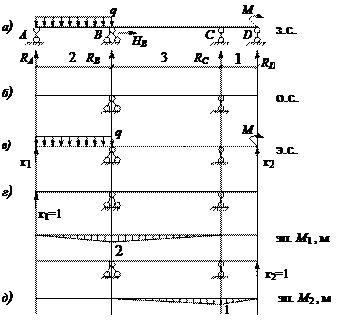
Рассмотрим статически неопределимую балку (рис. 20.3.1, а), нагруженную произвольной нагрузкой, назовем ее заданной системой (з.с.).

1. Определим степень статической неопределимости заданной системы: в балке возникает 5 опорных реакций, уравнений равновесия можно составить только 3, тогда 5 – 3 = 2 – балка дважды статически неопределима.

2. Выбираем основную систему (о.с.), для этого отбросим 2 лишние связи так, чтобы балка стала статически определимой (рис. 20.3.1, б).

3. Покажем эквивалентную систему (э.с.), приложив к основной системе заданную нагрузку и реакции отброшенных связей – x ₁, x ₂ (рис. 20.3.1, в).

4. Составим уравнения совместности деформаций. Принимаем принцип независимости действия сил (принцип суперпозиций), загружая о.с. поочередно силами x ₁ = 1; x ₂ = 1; заданной нагрузкой q, F.

Рассмотрим деформацию основной системы под действием силы x ₁ = 1 (рис. 20.3.1, г).

Обозначим:

δ₁₁ – перемещение точки приложения силы x ₁ по направлению этой силы под действием силы x ₁ = 1;

δ₂₁ – перемещение точки приложения силы x ₂ по направлению этой силы под действием силы x ₁ = 1.

Рассмотрим деформацию основной системы под действием силы х ₂ = 1 (рис. 20.3.1, д):

δ₁₂ – перемещение точки приложения силы х ₁ по направлению этой силы под действием силы x ₂ = 1.

δ₂₂ – перемещение точки приложения силы х ₂ по направлению этой силы под действием силы x ₂ = 1.

Рассмотрим деформацию основной системы под действием заданной нагрузки (рис. 20.3.1, е):

Δ_{1 F} – перемещение точки приложения силы x ₁ по направлению этой силы под действием заданной нагрузки.

Δ_{2 F} – перемещение точки приложения силы x ₂ по направлению этой силы под действием заданной нагрузки.

Однако на заданную систему силы действуют одновременно, причем значение сил х ₁ и х ₂ неизвестно.

Рассмотрим перемещение сечения В (точки приложения силы х ₁):

δ₁₁ х ₁ – перемещение точки приложения силы x ₁ от силы x ₁.

δ₁₂ х ₂ – перемещение точки приложения силы x ₁ от силы x ₂.

Δ_{1 F} – перемещение точки приложения силы x ₁ от заданной нагрузки.

В заданной системе в сечении В расположена опора, следовательно, перемещение этого сечения равно нулю, т. е.

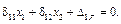(20.3.1)

Это и есть уравнение совместимости деформаций.

Аналогично можно составить уравнение совместимости деформаций для сечения С (точки приложения силы х ₂):

δ₂₁ – перемещение точки приложения силы x ₂ под действием силы x ₁;

δ₂₂ – перемещение точки приложения силы х ₂ под действием силы x ₂;

Δ_{2 F} – перемещение точки приложения силы x ₂ под действием заданной нагрузки, тогда

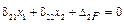. (20.3.2)

Это второе необходимое уравнение совместимости деформаций.

Перемещения δ₁₁, δ₁₂, δ₂₁, Δ_{1 F}, Δ_{2 F} определяются любым известным методом (интеграл Мора, правило Верещагина). На практике обычно применяют правило Верещагина (перемножение эпюр). Для этого необходимо в основной системе построить эпюры моментов от x ₁ = 1 (эп. 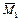), от х ₂ = 1 (эп. 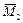), от заданной нагрузки (эп. M_F), а затем эти эпюры попарно перемножить по правилу Верещагина в соответствии с индексами перемещений: для определения Δ_{1 F} нужно эпюру 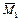перемножить с эпюрой M_F; для определения Δ_{2 F} эпюру 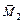перемножить с эпюрой M_F; δ₁₂ – эпюру 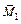перемножить с эпюрой 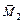и т. д.

5. Раскрываем статическую неопределимость балки, решая систему уравнений (20.3.1 и 20.3.2):

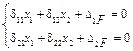, (20.3.3)

определяем x ₁ (R_B); x ₂ (R_C).

Остальные опорные реакции H_A, R_A, M_A можно определить из уравнений статики.

Следует отметить, что система уравнений (20.3.3) справедлива для любого количества неизвестных, ее можно записать в общем виде (20.3.4), и называется она системой канонических уравнений метода сил.

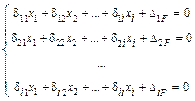, (20.3.4)

где i – степень статической неопределимости балки.

Так, если балка один раз статически неопределима (i = 1), то (20.3.4) имеет вид:

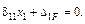
После определения опорных реакций строят эпюры конечных сил Q и изгибающих моментов M в заданной системе.

Для проверки правильности раскрытия статической неопределимости необходимо перемножить по правилу Верещагина эпюру Материалов в заданной системе на любую единичную эпюру 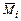в основной системе. В результате должен получиться ноль, т. к. перемещение по направлению опорной реакции в заданной системе невозможно (т. е. равно нулю).

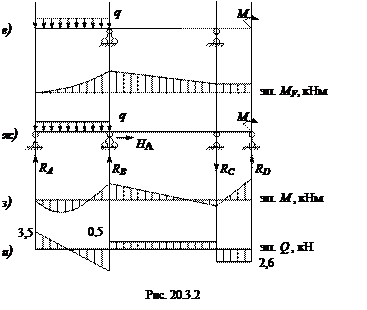
Пример 20.3.1. Построить эпюры Q и М в статически неопределимой балке (рис. 20.3.2, а), если q = 4 кН/м; М = 2 кН∙м.

Решение:

1. Раскроем степень статической неопределимости: реакций – 5 (R_A, H_B, R_B, R_C, R_D) (рис. 20.3.2, а); уравнений равновесия – 3 (Σ F_x = 0; Σ F_y = 0; Σ M_A = 0), т. е. 5 – 3 = 2 – балка дважды статически неопределима.

2. Выберем основную систему (рис. 20.3.2, б), отбросив «лишние» связи R_A и R_D.

3. Покажем эквивалентную систему (рис. 20.3.2, в).

4. Запишем систему канонических уравнений (уравнений совместимости деформаций):

.

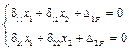Для определения коэффициентов и свободных членов канонических уравнений построим эпюры моментов в основной системе, применяя принцип суперпозиций, от х ₁ = 1 (эп. 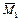) – рис. 20.3.2, г, от х ₂ = 1 (эп. 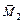) – рис. 20.3.2, д, от заданной нагрузки (эп. M_F) – рис. 20.3.2, е.

По правилу Верещагина определим коэффициенты и свободные члены канонических уравнений:

δ₁₁ – эпюру 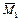перемножим с эпюрой :

;

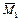δ₁₂ – эпюру 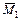перемножим с эпюрой :

;

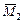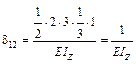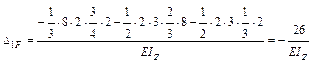
(знак минус у слагаемых потому, что эпюры 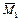и M_F имеют разные знаки);

δ₂₁ – эпюру 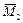перемножим с эпюрой :

,

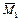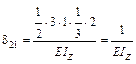можно сделать вывод, что δ₁₂ = δ₂₁, или δ _ik = δ _ki.

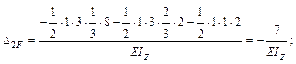
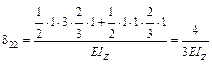
1. Решаем полученную систему уравнений:

,

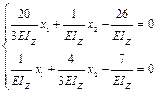получаем x ₁ = 3,5 кН; х ₂ = 2,6 кН.

2. Из уравнений статики определяем опорные реакции в балке (рис. 20.3.2, ж), если R_A = 3,5 кН; R_D = 2,6 кН:

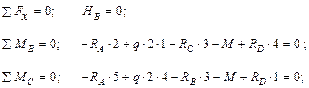
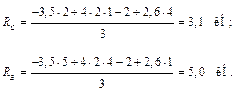
Проверка:

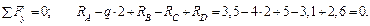
Построим эпюры M и Q в заданной системе (рис. 20.3.2, з, и).

Проверка:

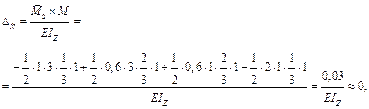
т. е. расчет выполнен верно.

Дата добавления: 2014-01-07