
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение напряжений
|
|
|
|
Для определения напряжений в балке произвольного сечения (рис. 21.2.1) используем принцип независимости действия сил.

|
Для этого разложим силу F на составляющие по главным центральным осям:
Fy = F cos α – вызывает изгиб относительно главной центральной оси z (в вертикальной плоскости);
Fz = F sin α – вызывает изгиб относительно главной центральной оси y (в горизонтальной плоскости).
Рассмотрим изгиб балки составляющей Fy (изгиб в вертикальной плоскости) (рис. 21.2.2).
 Максимальный изгибающий момент возникает в заделке и равен Mz = Fy∙l = F cos α l. Нейтральной линией является ось z, т. е. верхние волокна будут растянуты
Максимальный изгибающий момент возникает в заделке и равен Mz = Fy∙l = F cos α l. Нейтральной линией является ось z, т. е. верхние волокна будут растянуты 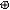 , а нижние сжаты , а нижние сжаты 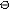 .
Напряжение в произвольной точке А (zA, yA): .
Напряжение в произвольной точке А (zA, yA):
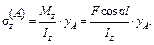 (21.2.1)
Рассмотрим изгиб балки составляющей Fz (изгиб в горизонтальной плоскости) (рис. 21.2.3). Максимальный изгибающий момент возникает
в заделке и равен My = Fzl = F sin α l.
Нейтральной линией является ось y, т. е. правые волокна будут растянуты (21.2.1)
Рассмотрим изгиб балки составляющей Fz (изгиб в горизонтальной плоскости) (рис. 21.2.3). Максимальный изгибающий момент возникает
в заделке и равен My = Fzl = F sin α l.
Нейтральной линией является ось y, т. е. правые волокна будут растянуты 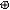 , а левые сжаты , а левые сжаты 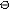 . Напряжение в той же точке А (zA, yA): . Напряжение в той же точке А (zA, yA):
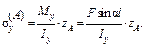 (21.2.2) (21.2.2)
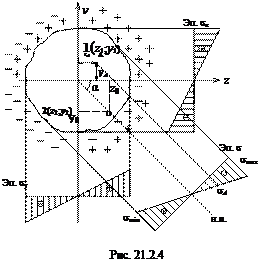
 На основании принципа независимости действия сил можно суммировать действия сил Fz и Fy (рис. 21.2.4) и сложить (21.2.1) и (21.2.2): На основании принципа независимости действия сил можно суммировать действия сил Fz и Fy (рис. 21.2.4) и сложить (21.2.1) и (21.2.2):
 (21.2.3) (21.2.3)
|
Из рис. 21.2.4 видно, что в первой четверти действуют только растягивающие напряжения, в третьей четверти – только сжимающие, следовательно, нейтральная линия может проходить только через вторую и четвертую четверти, т. к. только в них напряжения могут быть равны нулю.
Определим положение нейтральной линии. Так как по определению на нейтральной линии напряжения равны нулю, то из (21.2.3) имеем:
 ,
,
где y 0, z 0 – координаты точки, лежащей на нейтральной линии (рис. 21.2.4).
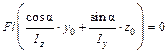 .
.
Так как Fl ≠ 0, то уравнение нейтральной линии имеет вид:
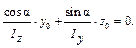 (21.2.4)
(21.2.4)
Как видно, это уравнение прямой линии, проходящей через начало координат (центр тяжести сечения). Положение нейтральной линии удобнее определить по углу φ, который она образует с осью z.
Согласно рис. 21.2.4, 
Из уравнения (21.2.4) имеем:
 (21.2.5)
(21.2.5)
Знак минус в (21.2.5) показывает, что силовая и нейтральная линии проходят через противоположные четверти, в дальнейшем этот знак упускают:
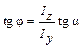 ,
,
где φ – угол между осью z и нейтральной линией; α – угол между осью y и силовой линией.
При косом изгибе момент инерции Iz не равен моменту инерции Iy. Если Iz = Iy (например, у круга, квадрата), то любая центральная ось является главной, и в этом случае имеет место прямой изгиб.
Наибольшие напряжения возникают в точках, наиболее удаленных от нейтральной линии (рис. 21.2.4), которые называются опасными точками (т. 1 и т. 2). Для определения этих точек необходимо провести касательные к контуру сечения параллельно нейтральной линии.
На основании (21.2.3) можно записать условие прочности:
 (21.2.8)
(21.2.8)
где R р R сж – расчетные сопротивления, соответственно, на растяжение и сжатие.
Если сечение прямоугольное (рис. 21.2.5), то опасными всегда будут угловые точки, например, 1 и 2, независимо от угла наклона нейтральной линии, тогда:
 ;
; 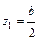 ;
; 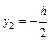 ;
;  ,
,
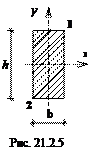 Следовательно, из (21.2.8) имеем:
Следовательно, из (21.2.8) имеем:
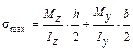 ,
,
но 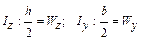 ,
,
тогда
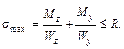 (21.2.9)
(21.2.9)
Следует отметить, что каждое слагаемое в формулах (21.2.8), (21.2.9) берется со своим знаком, который целесообразно устанавливать по характеру деформации, а значение изгибающих моментов и координат точек брать по модулю.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 314; Нарушение авторских прав?; Мы поможем в написании вашей работы!