Нормальные напряжения при чистом изгибе

Рассмотрим случай чистого изгиба кривого бруса, т. е. в поперечных сечениях возникают только изгибающие моменты, все остальные усилия равны нулю.

При выводе формул будем использовать гипотезы:

а) плоских сечений;

б) продольные волокна не давят друг на друга.

Рассмотрим кривой брус радиуса кривизны R (рис. 25.2.1).

Предположим, что нейтральная линия (н.л.) имеет радиус кривизны 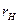, она смещена относительно центра тяжести сечения на некоторую величину . Проведем оси в сечении так, что ось направлена к центру кривизны бруса и проходит через центр тяжести сечения, а ось z совпадает с нейтральной линией, положение которой неизвестно. Задача является статически неопределимой.

Рассмотрим три стороны задачи:

1. Статическая сторона задачи

Рассечем брус поперечным сечением ав (рис. 25.2.1) на две части и рассмотрим сечение (рис. 25.2.2).

	Рис. 25.2.2

На элементарную площадку 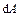, расположенную на расстоянии 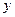от н.л., действует элементарное усилие 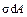(площадка находится в растянутой зоне):

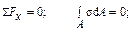(25.2.1)

(25.2.2)

2. Геометрическая сторона задачи

Выделим из кривого бруса элементарный участок abcd (рис. 25.2.1), которому соответствует до деформации элементарный угол 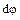, рассмотрим деформацию этого участка (рис. 25.2.3).

После деформации угол между сечениями ab и cd изменится на некоторую величину .

Произвольный слой АВ, расположенный на расстоянии 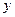от н.л. удлинится; если до деформации длина его была равна: полученное уравнение есть уравнение совместности деформаций, то после деформации удлинение его равно: , тогда относительное удлинение:

.

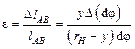3. Физическая сторона задачи

По закону Гука, напряжения прямо пропорциональны деформации:

(25.2.4)

или подставляя (25.2.3), получим:

(25.2.5)

Однако формулу (25.2.5) нельзя использовать для определения напряжений, т. к. в ней неизвестны r_H; ∆(dφ) и dφ.

Подставим (25.2.5) в (25.2.1):

.

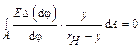Здесь

,

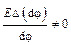следовательно

(25.2.6)

Подставим (25.2.5) в (25.2.2):

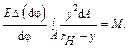(25.2.7)

Рассмотрим интеграл

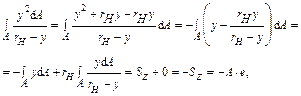(25.2.8)

где 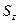– статический момент площади относительно нейтральной линии; А – площадь поперечного сечения,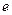– расстояние от ц.т. сечения до н.л., т. е.

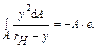(25.2.9)

Из уравнения (25.2.9) видно, что величина 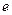всегда отрицательна, т. е. н.л. всегда смещена от ц.т. сечения к центру кривизны бруса. В дальнейшем будем учитывать абсолютные значения 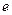и .

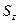Подставляя (25.2.9) в (25.2.7), получим:

или

(25.2.10)

Подставляя (25.2.10) в (25.2.5), имеем:

, (25.2.11)

где М – изгибающий момент в сечении; 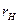– радиус кривизны н.л.;– расстояние от н.л. до слоя, в котором определяют напряжения.

Из формулы (25.2.11) видно, что наибольшие напряжения возникают в крайних точках сечения:

(22.2.12)

где и – радиусы кривизны соответственно внутреннего и внешнего слоя сечения (рис. 25.2.1); и 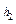– расстояния от н.л. до этих волокон.

Знаки напряжений легко установить по направлению изгибающего момента в сечении.

Дата добавления: 2014-01-07